БСЭ БСЭ - Большая Советская Энциклопедия (РИ)
- Название:Большая Советская Энциклопедия (РИ)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (РИ) краткое содержание
Большая Советская Энциклопедия (РИ) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Ритуально-мифологическая теория, восприняв многие идеи мифологической школы, утверждала, однако, приоритет ритуала над мифом (см. Мифология и Мифы ) и обосновывала исключительное значение ритуала в происхождении литературы, искусства, философии [античного театра, эпоса, философии, священной литературы Древнего Востока — в трудах «Кембриджской группы»; героического эпоса — Э. Миро, Ш. Отрана (оба Франция), Г. Р. Леви, Ф. Рэглана (оба Англия); романа, сказки — П. Сентива (Франция)]. Крайние формы теория обрела у Рэглана и Э. Хаймана (США); из их работ вытекало требование рассматривать ритуально-мифологические модели не как источник поэтической фантазии, а как её структуру. Исполнению такой задачи чрезвычайно содействовала теория архетипов Юнга, принятая поэтому на вооружение представителями собственно Р.-м. ш. [М. Бодкин (Англия), Н. Фрай (Канада), Р. Чейз и Ф. Уотс (США) и др.].
Опора на Юнга позволила школе распространить ритуалистический подход на всю историю искусства, включая современность (на школу оказало влияние «мифологизирование» в самой литературе 20 в.: Дж. Джойс, Т. Манн, Т. Элиот, У. Б. Йитс и др.). Р.-м. ш. ищет в произведениях не только мифологические мотивы, символы, метафоры, сознательные и бессознательные, но прежде всего воспроизведение определённых ритуальных схем, особенно обрядов инициации, эквивалентных, по её представлениям, психологическому архетипу смерти и нового рождения. Фрай утверждает абсолютное единство ритуала, мифа, архетипа и возводит к ним литературные образы и жанры, разрабатывая своеобразную «литературную антропологию». Он, например, соотносит 4 фазы природного цикла, отмеченные древними ритуалами, с мифами, архетипами, обрядами, жанрами, организованными в силу метафорического отождествления или ассоциаций по аналогии (так, например, увязываются: заря, весна, мифы о рождении героя, о воскресении, дифирамбическая и рапсодическая поэзия).
Важные результаты достигнуты ритуалистическим культуроведением и Р.-м. ш. в изучении литературных жанров, связанных генетически с ритуальными, мифологическими и фольклорными традициями, в анализе переосмысления древних поэтических форм и символов (рыцарский роман, античная и ренессансная драма, античная и библейская символика в поэзии, творчество У. Шекспира, Дж. Мильтона, У. Блейка). Некоторые аналогии в подходе к изучению традиции имеются в трудах советских учёных В. Я. Проппа, О . М. Фрейденберг, М. М. Бахтина. Однако в отличие от них западная Р.-м. ш. почти полностью сводит структуру литературного произведения к традиции и ищет ритуально-мифологическую основу во всех случаях. Литература и искусство растворяются, т. о., в мифе, миф — в ритуале [что вызывает протесты самих этнологов — У. Баскома, К. Клукхона, Дж. Фонтенроза (США)], литературоведение — в этнологии и психоанализе.
Лит.: Bodkin М., Archetypal patterns in poetry, 3 ed., N. Y., 1963; Chase R., Quest for myth, Baton Rouge, 1949; Frye N., Anatomy of criticism, Princeton, 1957; Myth and mythmaking, ed. by H. A. Murray, N. Y., 1960; Myth and symbol, Lincoln, [1963]; Myth and literature, ed. by J. Vickery, Lincoln, 1966; Fontenrose G., The ritual theory of myth, Berk, — Los Ang., 1966.
Е. М. Мелетинский.
Ритурнель
Ритурне'ль(франц. ritournelle, итал. ritornello, от ritorno — возвращение), 1) в вокальной музыке 17 — начала 18 вв. — короткие инструментальные разделы, выполняющие функции вступления, интермедии или коды. В некоторых случаях Р., прозвучавшая вначале как вступление, повторяется в конце в качестве коды. Если одна и та же Р. звучит не только в начале и конце, но и в середине произведения, она начинает играть роль рефрена. В современном итальянском языке термин «ритурнель» равнозначен термину «рефрен». 2) В танцевальной музыке — вступительный и заключительный отыгрыши в танце. 3) В балете конца 17 — начале 18 вв. — инструментальное вступление к танцу. 4) В поэзии Р. (риторнель) — особая трёхстишная строфа (преимущественно в итальянской народной и средневековой поэзии).
Ритца и Галёркина методы
Ри'тца и Галёркина ме'тоды,широко распространённые прямые методы решения главным образом вариационных задач и краевых задач математического анализа (см. Краевые задачи, Вариационное исчисление ) .
Метод Ритца применяется большей частью для приближённого решения вариационных задач и тех краевых задач, которые сводятся к вариационным. Пусть задан функционалV [ y ( x )] (или более сложный функционал) и требуется найти такую функцию у ( х ) , принимающую в точках x 0 и x i заданные значения a = у ( х 0 ) и b = у ( х 1 ) , на которой функционал V [ y ( x )] будет достигать экстремума. Значения исследуемого на экстремум функционала V [ y ( x )] рассматриваются не на всех допустимых в данной задаче функциях у ( х ) , а лишь на всевозможных линейных комбинациях вида
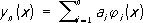
с постоянными коэффициентами a i ,составленных из n первых функций некоторой выбранной системы j 1( x ) , j 2( х ) ,..., j п ( х ) ,... (от удачного выбора этой системы функций зависит эффективность применения метода к решению конкретных задач). Необходимым условием выбора системы функций j 1( х ) является требование, чтобы функции у п ( х ) удовлетворяли условиям уп ( х о ) = a и y n ( x 1 ) = a для всех значений параметров a 1. При таком выборе функций у п ( х ) функционал V [ y ( x )] превращается в функцию Ф ( а 1, a 2,..., a n ) коэффициентов a i, последние выбирают так, чтобы эта функция достигала экстремума, т. е. определяют их из системы уравнений
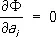
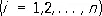 .
.
Например, пусть требуется решить задачу о минимуме интеграла
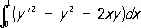
при условии y (0) = y (1) = 0. В качестве функций j i ( x ) можно взять x i (1 — х ) , тогда
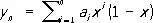 .
.
Если n = 2, то 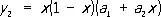 . Для определения коэффициентов a 1 и a 2получаем после вычислений два уравнения
. Для определения коэффициентов a 1 и a 2получаем после вычислений два уравнения
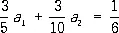 ;
;
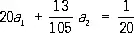 .
.
Интервал:
Закладка:
