Яков Перельман - Живая математика. Математические рассказы и головоломки

Получим

100 a + 10 b + c - ( a + b + c ) = 99 a + 9 b = 9(11 a + b ).

Но 9 (11 а + Ь) конечно, делится на 9; значит, при вычитании из числа суммы его цифр всегда должно получиться число, делящееся на 9 без остатка.

При выполнении фокуса может случиться, что сумма сообщенных вам цифр сама делится на 9 (например, 4 и 5). Это показывает, что зачеркнутая цифра есть либо

О, либо 9. Так вы и должны ответить: «О или 9».

Вот видоизменение того же фокуса: вместо того чтобы из задуманного числа вычитать сумму его цифр, можно вычесть число, полученное из данного какой-либо перестановкой его цифр. Например, из числа 8247 можно вычесть 2748 (если получается число большее задуманного, то вычитают меньшее из большего). Дальше поступают, как раньше сказано:

8247 - 2748 = 5499;

если зачеркнута цифра 4, то, зная цифры 5,9,9, вы соображаете, что ближайшее к 5 + 9 + 9, т. е. 23, число, делящееся на 9, есть 27. Значит, зачеркнутая цифра 27-23 = 4.

Вы предлагаете товарищу задумать трехзначное число, не оканчивающееся нулем, такое, в котором крайние цифры разнятся больше чем на 1, и просите затем переставить цифры в обратном порядке. Сделав это, он должен вычесть меньшее число из большего и полученную разность сложить с нею же, но написанною в обратной последовательности цифр. Ничего не спрашивая у загадчика, вы сообщаете ему число, которое у него получилось в конечном счете.

Если, например, было задумано 467, то загадчик должен выполнять следующие действия:

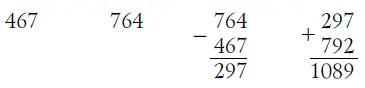
Этот окончательный результат - 1089 - вы и объявляете загадчику. Как вы можете его узнать?

Рассмотрим задачу в общем виде. Возьмем число с цифрами а, b, с. Оно изобразится так:

100а + 10 b + с.

Число с обратным расположением имеет вид:

100с + 10 b + а.

Разность между первым и вторым равна:

99а - 99с.

Делаем следующие преобразования:

99 а - 99 с = 99 (а - с) = 100 {а - с) - а + с = 100 (а - с) - 100 + 100 - 10 + 10 - а с = 100 (а - с - 1) + 90 + (10 - а + с).

Значит, разность состоит из следующих трех цифр:

цифра сотен: а - с - 1,

«десятков: 9,

«единиц: 10 + с - а.

Число с обратным расположением цифр изображается так:

100(10 + с - а) + 90 + (а - с - 1).

Сложив оба выражения

100 (а - с - 1) + 90 + 10 + с - а 100(10 + с - а) + 90 + а - с - 1,

получаем

100 х 9 + 180 + 9 = 1089.

Каковы бы ни были цифры а, Ь, с , в итоге выкладок всегда получается одно и то же число: 1089. Нетрудно поэтому отгадать результат этих вычислений: вы знали его заранее. Понятно, что показывать этот фокус одному лицу дважды нельзя - секрет будет раскрыт.

Для выполнения этого остроумного фокуса необходимо подготовить три какие-нибудь мелкие вещицы, удобно помещающиеся в кармане, например карандаш, ключ и перочинный ножик. Кроме того, поставьте на стол тарелку с 24 орехами; за неимением орехов годятся шашки, кости домино, спички и т. п.

Троим товарищам вы предлагаете во время вашего отсутствия в комнате спрятать в карман карандаш, ключ или ножик, кто какую вещь хочет. Вы беретесь отгадать, в чьем кармане какая вещь.

Процедура отгадывания проводится так. Возвратившись в комнату после того, как вещи спрятаны в карманах товарищей, вы начинаете с того, что вручаете им на сохранение орехи из тарелки.

Первому даете один орех, второму - два, третьему - три. Затем снова удаляетесь из комнаты, оставив товарищам следующую инструкцию. Каждый должен взять себе из тарелки еще орехов, а именно: обладатель карандаша берет столько орехов, сколько ему было вручено; обладатель ключа берет вдвое больше того числа орехов, какое ему было вручено; обладатель ножа берет вчетверо больше того числа орехов, какое ему было вручено.

Прочие орехи остаются на тарелке.

Когда все это проделано и вам дан сигнал возвратиться, вы, входя в комнату, бросаете взгляд на тарелку и объявляете, у кого в кармане какая вещь.

Фокус тем более озадачивает, что выполняется без участия тайного сообщника, подающего вам незаметные сигналы. В нем нет никакого обмана: он целиком основан на арифметическом расчете. Вы разыскиваете обладателя каждой вещи единственно лишь по числу оставшихся орехов. Остается их на тарелке немного - от 1 до 7, и счесть их можно одним взглядом.

Как же, однако, узнать по остатку орехов, кто взял какую вещь?

Очень просто: каждому случаю распределения вещей между товарищами отвечает иное число остающихся орехов. Мы сейчас в этом убедимся.

Пусть имена ваших товарищей Владимир, Георгий, Константин; обозначим их начальными буквами: В, Г, К Вещи также обозначим буквами: карандаш - а, ключ - Ь, нож - с. Как могут три вещи распределиться между тремя обладателями? На 6 ладов:

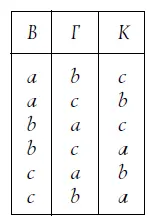
Других случаев, очевидно, быть не может; наша табличка систематически исчерпывает все комбинации.

Посмотрим теперь, какие остатки отвечают каждому из этих 6 случаев:

Вы видите, что остаток орехов всякий раз получается иной. Поэтому, зная остаток, вы легко устанавливаете, каково распределение вещей между вашими товарищами. Вы снова - в третий раз - удаляетесь из комнаты и заглядываете там в свою записную книжку, где записана сейчас воспроизведенная табличка (собственно, нужны вам только первая и последняя графы); запомнить ее наизусть трудно, да и нет надобности. Табличка скажет вам, в чьем кармане какая вещь. Если, например, на тарелке осталось 5 орехов, то это означает (случай b, с, а ), что

ключ - у Владимира;

нож - у Георгия;

карандаш - у Константина.

Чтобы фокус удался, вы должны твердо помнить, сколько орехов вы дали каждому товарищу (раздавайте орехи поэтому всегда по алфавиту, как и было сделано в нашем случае).

Почему 28 костей домино можно выложить с соблюдением правил игры в одну непрерывную цепь?

Когда 28 костей домино выложены в цепь, на одном ее конце оказалось 5 очков.

Сколько очков на другом конце?

Ваш товарищ берет одну из костей домино и предлагает вам из остальных 27 составить непрерывную цепь, утверждая, что это всегда возможно, какая бы кость ни была взята. Сам же он удаляется в соседнюю комнату, чтобы не видеть вашей цепи.