Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

В своей книге «Дух порядка. Исследование психологии декоративных искусств» австрийский историк искусства Эрнст Гомбрих описывает кельтские узлы. Их особенность заключается в том, что нить проходит через все выделенные точки на каждой стороне сетки с квадратными ячейками и возвращается в исходное положение.

Бесконечный узел — это узел, начало и конец которого совпадают:

Кельтские узлы не всегда являются бесконечными, или циклическими:

Возникает вопрос: почему одни узлы бесконечные, а другие — нет? Перед тем как начать поиск ответа, рассмотрим, как строятся такие узлы. Их основой является сетка с квадратными ячейками, на сторонах которых выбирается последовательность точек, через которые проходит нить узла:

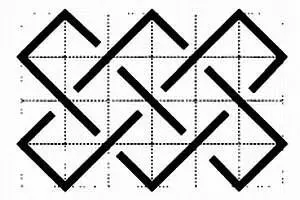
За счет этого узлы можно описывать числом вершин на каждой из сторон сетки, через которые проходит нить узла. Первый из улов, представленных выше, — узел 3 x 2, второй — 3 x 3, последний — 6 x 4. Узел 3 x 2 располагается на сетке размером 6 х 4 и проходит через вершины 1–3–3 в горизонтальных рядах и через вершины 1–3 — в вертикальных рядах. Сетка 6 x 4 понимается как (1 + 2·2 + 1) х (1 + 2 + 1). Остальные узлы описываются аналогично. Узел 3 x 3 располагается на сетке 6 х 6 = (1 + 2·2 + 1) х (1 + 2·2 + 1), узел 6 x 4 — на сетке 12 х 8 = (1 + 2·5 + 1) х (1 + 2·3 +1).

Можно сказать, что ответ на вопрос, будет ли узел бесконечным, зависит от числа вершин, через которые проходит нить на каждой стороне сетки. Узел 3 х 2 является бесконечным, так как образован одной нитью. Узел 3 х 3 не является бесконечным, так как состоит из трех нитей. Узел 6 x 4 также не является бесконечным и состоит из двух нитей.

В чем же ключ к решению задачи? Нить смещается влево, вправо, вверх и вниз. Если бы мы не ограничивались одним прямоугольником, а продолжили узел дальше по вертикали и по горизонтали, то смогли бы понять суть проблемы. Рассмотрим узел (3 х 2):

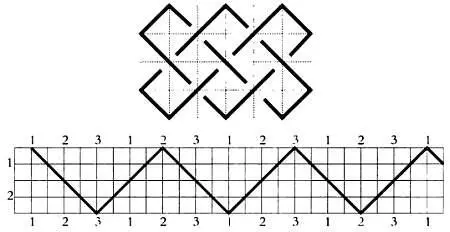
Мы начинаем с точки 1, затем, сместившись на две единицы вправо, попадаем в 3, затем в 2 и наконец снова в 1. Получается числовая последовательность, которая циклически повторяется до бесконечности:

[1, 3, 2] = 1, 3, 2, 1, 3, 2, 1, 3, 2, 1…

На сетке размером (4 х 2) требуется два таких цикла:

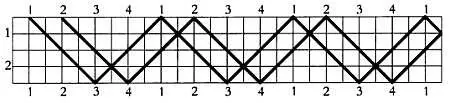
В первом случае мы перепрыгиваем через две клетки. Полный цикл завершается после шести шагов, когда мы возвращаемся в исходную точку 1. Мы обошли все цифры 1, 2 и 3. Во втором случае для обхода всех цифр требуется два цикла:

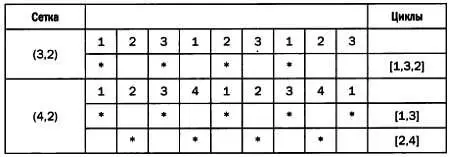
Почему? Потому что 4 делится на 2. Если мы начинаем цикл в точке 1, то мы всегда будем проходить через точки 1 и 3 и никогда — через 2 и 4. Для этого потребуется новый цикл с началом в точке 2. В предыдущем случае цикл завершается после 6 = НОК (3, 2) этапов, и требуется всего один цикл, так как НОД (3, 2) = 1.

Это же происходит и в примере с сеткой 6 x 4, где НОД (6, 4) = 2 цикла, и на сетке 3 х 3, где число циклов равно 3 = НОД (3, 3). Подведем итог.

Теорема: На сетке размером ( m, n ) число циклов равно НОД ( m, n ).

Следствие 1: Если m и n — взаимно простые, то на сетке ( m, n ) имеется единственный бесконечный цикл.

Следствие 2: На сетке размером ( m, n ) число петель равняется 2 х ( m + n ).

При посадке деревьев в шахматном порядке саженцы располагаются в вершинах воображаемых равносторонних треугольников — это гарантирует, что все деревья будут располагаться друг от друга на одинаковом расстоянии:

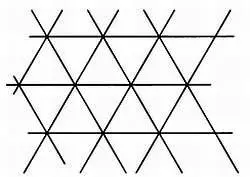
Если математику дать задачу о построении подобной сетки с треугольными ячейками, он, скорее всего, начнет искать способ построения равносторонних треугольников, применимый на практике, и буквально со стопроцентной вероятностью предложит евклидово решение, приведенное в предложении 1 книги I «Начал».

Предложение 1 из «Начал» Евклида: построение равностороннего треугольника на данном отрезке АВ.

Для этого построения нужно заменить циркуль веревкой, длина которой равна длине стороны искомого треугольника. Садовод должен обходить участок, проводя дуги окружностей и отмечая точки их пересечения.

Сначала он отметит точки на одной прямой, равноудаленные друг от друга:

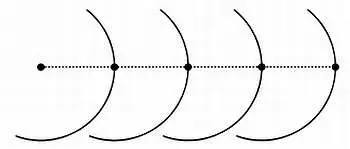
Затем, использовав каждую из этих точек в качестве центра окружности, он проведет дуги, которые пересекутся в вершинах равносторонних треугольников:

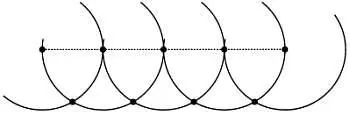
В результате садовод определит, где нужно посадить деревья.

Так эту задачу решил бы математик. Однако, согласно Жиль-Альберу (1999), садоводы строят сетку из треугольных ячеек следующим образом:

«Посадка в шахматном порядке <���…>. Чтобы определить, где следует сажать деревья, достаточно, чтобы один рабочий взял в руки рулетку и встал там, где нужно посадить первое дерево. Второй рабочий, взяв в руки конец рулетки, должен отойти на расстояние, равное желаемому расстоянию между деревьями (например, 5 м) и отмотать ленту длиной в два раза больше чем требуется (если деревья планируется посадить на расстоянии 5 м друг от друга, рабочий должен отмотать 10 м ленты рулетки). Третий рабочий должен взяться за середину ленты рулетки и отойти в сторону, натягивая ленту. Когда лента рулетки натянется полностью, третий рабочий окажется точно в том месте, где нужно посадить третье дерево».

Здесь равносторонний треугольник понимается как частный случай равнобедренного. Именно на этом примере можно оценить справедливость фразы: теоретическое решение практической задачи обычно является не лучшим практическим решением. Вот и в этом случае решение, предложенное профессиональным математиком, на практике не применяется. С математической точки зрения, напротив, практика не имеет значения. Не имеет значения и то, что в практическом решении равносторонний треугольник понимается иначе — для математика это не новость.