Александр Казанцев - Том (7). Острие шпаги
- Название:Том (7). Острие шпаги
- Автор:
- Жанр:
- Издательство:Молодая гвардия
- Год:1984
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Казанцев - Том (7). Острие шпаги краткое содержание
Социально-фантастический и приключенческий роман известного советского писателя, главным героем которого является французский математик Ферма, сформулировавший в свое время увлекательную и нерешенную до сих пор проблему теории чисел. В книге помещены четыре рассказа автора.
Иллюстрации художника Ю. Г. Макарова.
http://ruslit.traumlibrary.net
Том (7). Острие шпаги - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
29
Швейцарская легенда повествует о необычайно метком стрелке, народном герое Вильгельме Телле, которого враги принудили сбить стрелой яблоко с головы любимого сына. (Примеч. авт.)
30
Переписка ученых, собранная Джоном Валлисом, вошла приложением к третьему тому сочинений Пьера Ферма на французском языке в 1679 году, выпущенных его сыном Самуэлем. (Примеч. авт.)
31
Это письмо к Каркави получило название «Завещание Ферма». (Примеч. авт.)
32
Примечание автора для особо интересующихся. Рассмотренный Паскалем «бином», впоследствии названный «биномом Ньютона», известен ныне как:
(x + y) 0= 1;
(x + y) 1= z;
(x + y) 2= x 2+ 2xy + y 2;
(x + y) 3= x 3+ 3x 2у + 3xy 2+ y 3;
(x + y) 4= x 4+ 4x 3y 2+ 6x 2y2 + 4xy 3+ y 4
и т. д.
33
В своем 42-м замечании на полях книги «Арифметика» Диофанта Пьер Ферма записал по-латыни: «…наука о целых числах, которая, без сомнения, является прекраснейшей и наиболее изящной, не была до сих пор известна ни Боше, ни кому-либо другому, чьи труды дошли до меня» (Боше де Мазариак – математик, издавший в переводе на латынь с древнегреческого «Арифметику» Диофанта, снабдив ее своими комментариями и дополнениями, ставшую настольной книгой Ферма). (Примеч. авт.)
34
Примечание автора для особо интересующихся .
Метод совмещенных парабол Пьера Ферма сводится к тому, что в системе прямоугольных координат (декартовых!) с горизонтальной осью x и вертикальной q – (x0 1q) – вычерчивается парабола по уравнению q = x n. Чертеж поворачивается на 180º, и на нем наносится (см. рис.) еще одна система прямоугольных координат (y0 1l) с горизонтальной осью «у» и вертикальной «l».
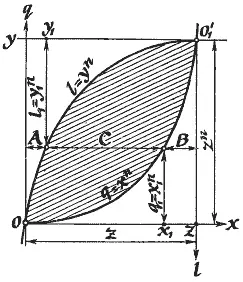
Вертикальные оси двух систем координат отстоят одна от другой на величину z, а горизонтальные на z n. В перевернутой системе координат тоже вычерчивается точно такая же парабола по уравнению l = y n. Две совмещенные таким способом параболы образуют полусимметричную геометрическую фигуру, ограниченную ими. Выбирая точку x 1на оси x, строим от нее вертикальный отрезок (до пересечения с первой построенной параболой) с длиной g 1= X 1 n. Проведя теперь горизонтальную линию от пересечения вертикального отрезка с параболой через фигуру до второй параболы, получим точку, вертикальный отрезок от которой до оси у перевернутой координатной системы отметим на оси y точку y 1. Длина же этого отрезка, равная ординате перевернутой параболы, будет l = y n. Из построения следует: q + l 1= x 1 n+ y 1 n= z 1 n. Диофантово уравнение, положенное Ферма в основу его Великой теоремы. Все это восстановлено А. Н. Кожевниковым.
35
Примечание автора для особо интересующихся . По просьбе автора вывод «бинома Ферма» выполнен заслуженным деятелем науки и техники РСФСР доктором технических наук профессором М. М. Протодьяконовым следующим образом. Из основной формулы x n+ y n= z nи вышеприведенного рисунка следует: (A + B + C) n= (A + C) n+ (B + C) n. После умножения обеих частей уравнения на множитель меньше единицы
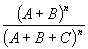
после объединения одинаковых степеней, раскрытия малых скобок, очевидных сокращений и преобразований:
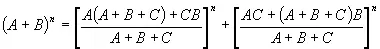
после сокр. прав. части
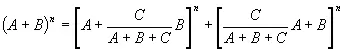
Обозначив через
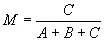
получаем « Бином Ферма »: (A + B) n= (A + MB) n+ (MA + B) n, может быть, несправедливо забытый современными математиками, но восстановленный А. Н. Кожевниковым.
36
Лишь Эйлер в следующем веке показал, что эта дробь, если «a» целое и неквадратное число, будет периодической. (Примеч. авт.)
37
Задача эта сводится к выражению x n+ y n= z n. (Примеч. авт.)
38
Великая теорема Ферма. (Примеч. авт.)
39
В 45-м замечании к книге Диофанта Ферма даст развернутое доказательство нерешаемости для четвертой степени уравнения: x 4+ y 4= z 4в целых числах, к чему мы еще вернемся. Еще раньше, в 33-м замечании, говоря о Диофанте, Ферма написал: «Почему же он не ищет двух биквадратов, сумма которых равна квадрату? Конечно, потому, что эта задача невозможна, как это с несомненностью показывает наш метод доказательства». (Примеч. авт.)
40
Примечание автора для особо интересующихся.
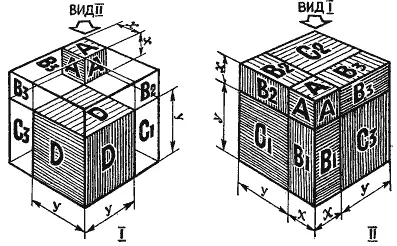
Графическое решение «бинома Ньютона в третьей степени» представлено на рисунке, выполненном заслуженным деятелем науки и техники РСФСР доктором технических наук профессором М. М. Протодьяконовым. Куб у него складывается из кубов, среднего со стороной y и малого со стороной x, расположенных по диагонали большого куба, со стороной x + y, трех пластин объемом x 2y и трех брусков объемом x 2y, точно заполняющих оставшиеся в большом кубе места от двух первых кубов. Объемы всех этих фигур соответствуют: (x + y) 3= x 3+ 3x 2y + 3xy 2+ y 3.
41
Примечание автора для особо интересующихся. «Метод спуска» Ферма изложен в его 45-м примечании к «Арифметике» Диофанта и в его письме к Каркави, где для доказательства того, что площадь прямоугольного треугольника не может быть равна квадрату целого числа, говорилось: «Если бы существовал некоторый прямоугольный треугольник в целых числах, который имел бы площадь, равную квадрату, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством. Если бы существовал второй, меньший первого, который имел бы то же свойство, то существовал бы, в силу подобного рассуждения, третий, меньший второго, который имел бы то же свойство, и, наконец, четвертый, пятый, спускаясь до бесконечности. Но если задано число, то не существует бесконечности по спуску меньших его (я все время подразумеваю целые числа). Откуда заключаю, что не существует никакого прямоугольного треугольника с квадратной площадью».
Этим методом доказаны частные случаи для степеней = 3 и 4.
42
Примечание автора для особо интересующихся. «Метод подъема» гипотетически мог бы быть изложен так:
Если прямоугольный треугольник можно построить только на плоскости, имеющей два измерения, и свойством такого «плоского места» будет пифагоров закон о том, что квадрат гипотенузы равен сумме квадратов катетов, то нет оснований полагать, что подобные «законы» отражают свойства «пространственных» и «субпространственных мест» с тремя и более измерениями, что при переходе (подъеме) от плоскости к объему (кубу, параллелепипеду или другой пространственной фигуре) диагональ, скажем куба, возведенная в третью степень, будет равна сумме других отрезков, укладывающихся в эту фигуру (сторон куба) в третьей степени. И еще меньше оснований полагать, что при переходе к «невообразимым фигурам» четырех и больше измерений можно найти целочисленное решение для четвертой степени одного отрезка, равного сумме двух других отрезков в четвертых степенях каждый. Для необоснованности подобных предположений достаточно доказать, что целочисленных решений нет, скажем, для биквадратов, что и будет общим доказательством отсутствия целочисленных решений для «пространственных» и «субпространственных» фигур вообще.
Читать дальшеИнтервал:
Закладка:










