Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс

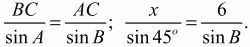
Учитывая, что сумма углов в треугольнике равна 180°, получим:?В = 180° – ?A – ?C = 180°– 45°– 105° = 30°.

Итого

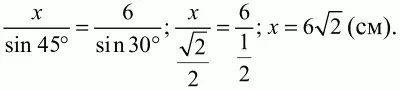
Ответ:

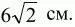
3. Найдите площадь треугольника со сторонами 2, ?5 и 3 (рис. 128). (1)

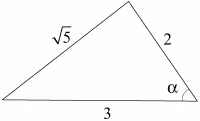
Рис. 128.

Решение. Можно воспользоваться формулой Герона:

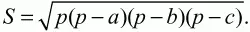
В нашем случае:

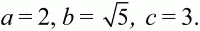
Полупериметр:

Проще решить задачу можно было бы так. По теореме косинусов:

Так как площадь треугольника равна половине произведения двух сторон на синус угла между ними, то:

Ответ: ?5.

4. В треугольнике ABC, где ?ACB = 120°, проведена медиана СМ. Найдите ее длину, если АС = 6, ВС = 4 (рис. 129). (2)

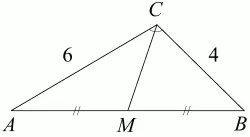
Рис. 129.

Решение. Воспользуемся формулой длины медианы

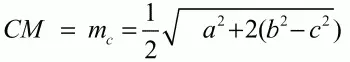
У нас а = ВС = 4, b = АС = 6. Осталось найти с = АВ. Применим к треугольнику АСВ теорему косинусов: с2= АВ2= АС2+ ВС2– 2AC ? BC ? cos(?АСВ) = 62+ 42– 2 ? 6 ? 4 ? cos 120° = 36 + 16–48?(-1/2) = 76.

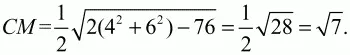
Ответ: ?7.

5. Найдите длины сторон АВ и АС остроугольного треугольника ABC, если ВС = 8, а длины высот, опущенных на стороны АС и ВС, равны 6, 4 и 4 соответственно (рис. 130). (2)

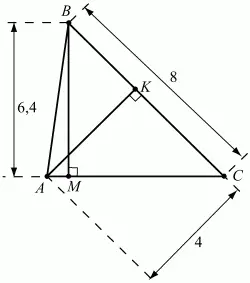
Рис. 130.

Решение. Единственный угол треугольника, который остался «нетронутым», угол С.

Из прямоугольного треугольника ВМС следует:

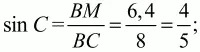
тогда

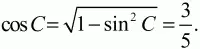
Из ?АКС:

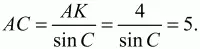
А теперь по теореме косинусов, применённой к треугольнику ABC, получаем:

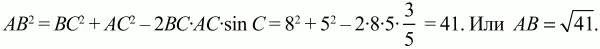
Ответ: AB = ?41; AC = 5.

6. В треугольнике, один из углов которого равен разности двух других, длина меньшей стороны равна 1, а сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найти длину большей стороны треугольника (рис. 131). (2)

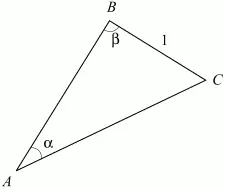
Рис. 131.

Решение: Обозначим через ? наименьший угол в треугольнике и через ? наибольший угол. Тогда третий угол равен ? – ? – ?. По условию задачи ? – ? = ? – ? – ? (больший угол не может равняться разности двух других углов). Отсюда следует, что 2? = ?; ? = ?/2. Значит, треугольник прямоугольный. Катет ВС, лежащий против меньшего угла ?, равен по условию 1, значит, второй катет АВ равен ctg?, а гипотенуза АС равна 1/sin ?. Поэтому сумма площадей квадратов, построенных на гипотенузе и большем катете, равна:

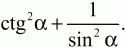
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, и её радиус равен:

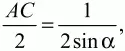
а площадь равна:

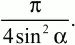
Пользуясь условием задачи, имеем уравнение:

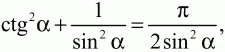
откуда

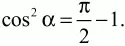
Длина большей стороны треугольника равна

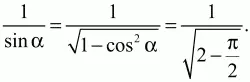
Ответ:

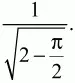
7. Длины сторон а, b, с треугольника равны 2, 3 и 4. Найти расстояние между центрами описанной и вписанной окружностей. (2)

Решение. Для решения задачи даже чертеж не нужен. Последовательно находим: полупериметр

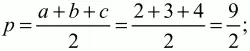
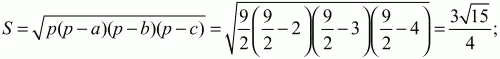
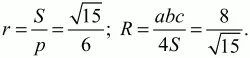
Расстояние между центрами окружностей:

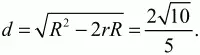
Ответ:

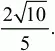
8. В треугольнике ABC величина угла ВАС равна ?/3, длина высоты, опущенной из вершины С на сторону АВ, равна ?3 см, а радиус окружности, описанной около треугольника ABC, равен 5 см. Найти длины сторон треугольника ABC (рис. 132). (3)

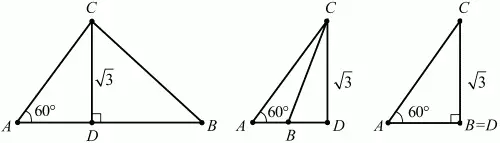
Рис. 132.

Решение: Пусть CD – высота треугольника ABC, опущенная из вершины С. Возможны три случая. Основание D высоты CD попадает:

1) на отрезок АВ;

2) на продолжение отрезка АВ за точку В;

3) в точку В.

По условию радиус R окружности, описанной около треугольника ABC, равен 5 см. Следовательно, во всех трех случаях:

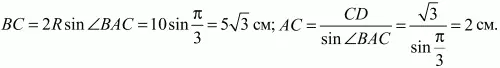
Теперь ясно, что точка D не совпадает с точкой В, так как ВС ? CD. Применяя теорему Пифагора к треугольникам ACD и BCD, находим, что