Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Название:Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Андрей Павлов - Геометрия: Планиметрия в тезисах и решениях. 9 класс краткое содержание
В пособии конспективно изложен школьный курс геометрии. Приведены комплекты экзаменационных билетов, задачи и их решения, распределённые по различным уровням сложности.
Материалы пособия соответствуют учебной программе школьного курса геометрии.
Для учителей и учащихся 9-х классов.
Геометрия: Планиметрия в тезисах и решениях. 9 класс - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
На рис. 5 угол ? = ?АОВ образован двумя отрезками ОА и ОВ.
На рис. 6 угол ? образован двумя лучами р и q, имеющими начальную точку О.
Если стороны угла являются дополнительными лучами одной прямой, то угол называют развёрнутым (рис. 7).

Рис. 7.
Угол А является здесь развёрнутым.
Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок, соединяющий любые две точки, лежащие на разных сторонах угла.
Луч q проходит между сторонами ОА и OB угла AOB (рис. 8).
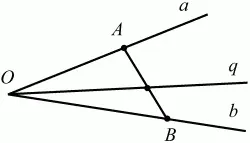
Рис. 8.
Углы измеряют в градусах и радианах. При этом ? радиан = 180°.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами (рис. 9).
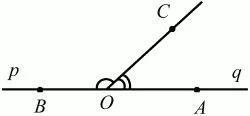
Рис. 9.
Сумма смежных углов равна 180°.
Лучи p и q – дополнительные, точка В принадлежит лучу p а точка А принадлежит лучу q. Углы СОА и СОВ – смежные.
Угол, равный 90°, называется прямым.
Угол, меньший 90°, называют острым углом. Угол, больший 90° и меньший 180°, называют тупым (рис. 10, а; б; в).
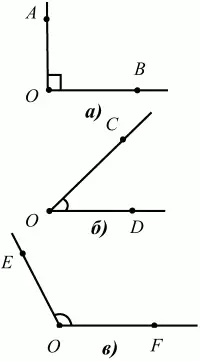
Рис. 10.
Углы:?АОВ – прямой, ?COD – острый, ?EOF – тупой.
На рисунках прямые углы часто обозначают знаками ?, ?.
Два угла называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого (рис. 11).
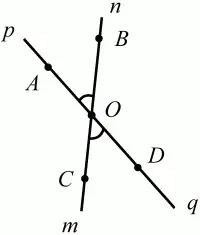
Рис. 11.
р и q – дополнительные лучи одной прямой, а m и n – дополнительные лучи другой прямой. Точка О – точка пересечения этих двух прямых и является начальной точкой всех указанных выше лучей.
Точки А, В, С, D лежат на соответствующих лучах.
Углы АОВ и COD – вертикальные.
Две прямые называют перпендикулярными, если они пересекаются под прямым углом. Перпендикулярность прямых обозначается знаком ? (рис. 12):
а ? b.
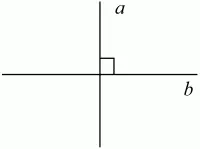
Рис. 12.
Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра (рис. 13):
АA' – перпендикуляр к прямой a, A' – обоснование перпендикуляра.
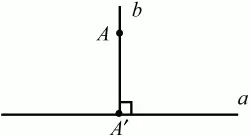
Рис. 13.
Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам (рис. 14).
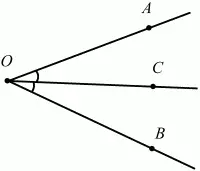
Рис. 14.
ОС – биссектриса угла АОВ (?АОС = ?ВОС).
Пусть две прямые a и b пересечены прямой с.
Прямая с по отношению к прямым a и b называется секущей (рис. 15).
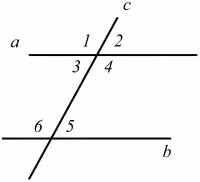
Рис. 15.
Углы 3 и 5 (4 и 6) называются внутренними накрест лежащими, углы 3 и 6 (4 и 5) – внутренними односторонними, углы 1 и 6 (2 и 5) – соответственными.
Две прямые называются параллельными, если они не пересекаются. Для обозначения параллельности прямых используется знак||(рис. 16):
а||b.

Рис. 16.
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами (рис. 17):
?ABC.
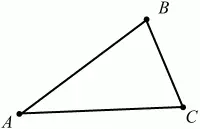
Рис. 17.
Углом треугольника ABC при вершине А называется угол, образованный отрезками АВ и АС. Также определяются углы треугольника при вершинах В и С.
Две фигуры называются равными, если они при наложении друг на друга совпадают (т. е. существует движение, переводящее одну фигуру в другую). Таким образом, треугольники равны, если у них соответствующие стороны и соответствующие углы равны (при этом соответствующие углы лежат против соответствующих сторон).
Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника (рис. 18).
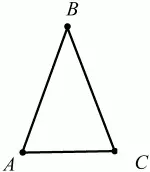
Рис. 18.
?ABC – равнобедренный (АВ = ВС – боковые стороны, АС – основание).
Треугольник, у которого все стороны равны, называется равносторонним (рис. 19).
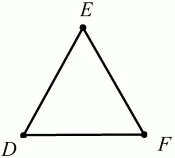
Рис. 19.
? DEF– равносторонний (DE = EF = DF).
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведённый из этой вершины к прямой, которая содержит противолежащую сторону треугольника (рис. 20, а; б).
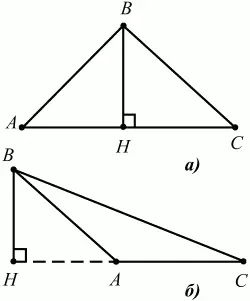
Рис. 20.
ВН – высота в треугольнике ABC (ВН ? АС).
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне (рис. 21).
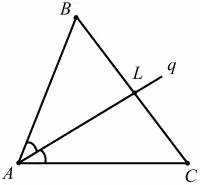
Рис. 21.
AL – биссектриса в треугольнике ABC (?BAL = ?CAL).
Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника (рис. 22).
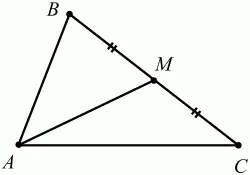
Рис. 22.
AM – медиана треугольника ABC (BM = MC).
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (рис. 23).

Рис. 23.
? – внешний угол ?ABC при вершине А.
Треугольник называется прямоугольным, если у него есть прямой угол (рис. 24).
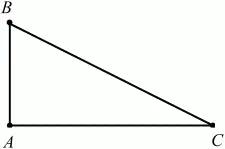
Рис. 24.
Читать дальшеИнтервал:
Закладка: