Н. Федотов - Мир приключений, 1927 № 05

ГЛ. КОНТОРА И РЕДАКЦИЯ: ЛЕНИНГРАД, СТРЕМЯННАЯ 8

ИЗДАТЕЛЬСТВО «П. П. СОЙКИН»

Ленинградский Гублит № 36855.

Зак. № 743.　

Тип. Л.С. П. О. Ленинград. Лештуков, 13.

Тираж — 30000 экз.　

«НЕ ПОДУМАВ, НЕ ОТВЕЧАЙ!»*

О ЛИТЕРАТУРНОМ КОНКУРСЕ

3-я стр. обложки

«ЗВЕРЬ И ЧЕЛОВЕК»,

— рассказ Н. И Федотова , иллюстрации И. А. Владимирова 　

«ЗАКОН ПРАВДЫ»,

— рассказ Адели-Сент-Джонс , перевод Н. Мохначева ,

иллюстр. Ч. Митчеля

«АТАВИСТИЧЕСКИЕ УКЛОНЫ БУССА»,

— рассказ Н. И. Муханова , иллюстрации С. М. Мочалова

«ФИЛЬКА БЕСШТАННЫЙ РАК»,

— рассказ Н. Комарова , иллюстрации Н. Кочергина

«НА ДАЛЕКИХ ОКРАИНАХ». «ЛЮДОЕДЫ»,

— рассказ из таежной жизни Павла Белецкого ,

иллюстр. И. А. Владимирова

«РАСЧЕТ ИЛИ СЧАСТЬЕ?»

— рассказ Д. Мак-Кейля , иллюстрации Д. Вилькинсона

«ЖУТКИЙ ВЕЧЕР»

— гротеск　 А. М. Фрея , перевод Р. Ф. Куллэ ,

иллюстр. В. Т. Калягина и Н. Т. Суворова

«ТАЙНОЕ УБЕЖИЩЕ»,

очерк из жизни слонов Поля Анникстера

в переработке Н. Николаева , иллюстр. С. Тресилиан 　

«ОТ ФАНТАЗИИ К НАУКЕ»

—　«Откровения науки и чудеса техники».　

«ЗАГАДКА МАРСА»

— очерк П. Мордвинова с иллюстрациями 　

• «Пуля изобличитель»

• «Новости в музыке», с иллюстрациями 　

• «Новости спорта», — с иллюстрациями 　

Обложка — художника И. А. Владимирова

* Примечание: для удобства верстки и чтения раздел «НЕ ПОДУМАВ, НЕ ОТВЕЧАЙ!» объединен вместе. В бумажном журнале он разделен на четыре части.

Задача № 31.

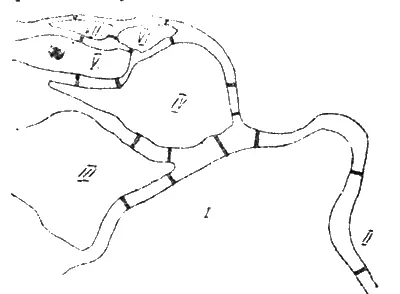
В Кенигсберге, в Германии, есть остров, называемый Кнейпгоф. Омывающие его реки делятся на два рукава, образуя фигуру помещенного здесь рисунка Через эти рукава переброшены семь мостов. Два студента побились об заклад, что все эти мосты можно обойти, проходя каждый из них не более одного раза. Сказано-сделано, но тот, кто хотел это сделать, вскоре убедился, что дело не так просто, как это кажется. И пари было им проиграно. — Попробуйте, может быть вы окажетесь сообразительней. Задача стоит того, чтобы над ней доломать голову; по крайней мере знаменитый математик Эйлер, живший в конце 18 века, посвятил ей целый математический труд, где нашел правила, когда и при каких случаях возможен такой однократный обход мостов.

Задача № 32.

Но город Кенигсберг далеко, и мы привели задачу о его мостах, как имеющую исторический характер. Гораздо интереснее попробовать свои силы на обходе хотя бы Ленинградских мостов и островов. Перед вами (рис. 2) схематическая карта Ленинграда; пренебрегая каналами и протоками, попробуйте обойти 18 Ленинградских мостов по одному разу. Попробуйте это сделать наудачу, а если не удастся, прибегните к правилу Эйлера, приведенному в решении первой задачи.

Задача № 33

Две хозяйки встретились в мануфактурном магазине. — Уж право, я не знаю на чем остановиться — сказала одна — за пять с полтиной я могу купить сатина на четыре метра больше, чем полотна на четыре с полтиной… — Знаете что? — отвечала другая — мой совет: возьмите и того, и другого, цена не дорогая и товар скоро расхватают. Возьмите и того, и другого по 10 метров — тогда вся покупка вам обойдется в 15 рублей. Сообразите в 10 минут, почем продавались полотно и сатин?

Задача № 34　

Вот общеизвестная фигура правильного, т. называемою греческого креста. Разрежьте его через середину на три части таким образом, чтобы, сложив их, вы получили бы прямоугольник, у которого одна сторона вдвое длиннее другой стороны. Если вы решите эту задачу в 10 минут, значит у вас хорошее уменье комбинировать формы.　

Задача № 35

Перед вами справа круг, разделенный на две симетричные и равные части — на темную и на светлую. Разбейте эту фигуру одной линией на четыре равные и одинаковые части.

Задача № 36.

Некий досужий остроумец, прочитав в «Красной Вечерней Газете» о путаных адресах на письмах, с которыми почтамту столько возни и хлопот, решил испытать сообразительность почты и отправил открытку со следующим «законспирированным» адресом. Почтовый служащий оказался, однако, неглупым малым, читавшим наш отдел «Не подумав — не отвечай», и в 5 минут разобрал адрес и направил письмо куда надо и тому самому лицу, которому оно было послано. Может быть вы окажетесь также сообразительны и легко расшифруете загадочный адрес?

К сведению подписавшихся на журнал «МИР ПРИКЛЮЧЕНИЙ» с рассрочкою платежа и уплативших не более трех рублей сообщается, что во избежание перерыва в получении журнала с №. 7-го, надлежит озаботиться высылкою доплаты. При высылке очередного взноса необходимо указать, что деньги высылаются в доплату к подписке № такой-то (обозначенный в верхнем левом углу ярлычка бандероли).

Задача № 31.

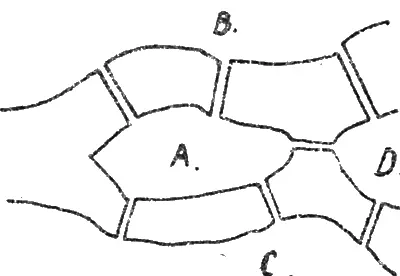
Не отчаивайтесь, читатель, если вам не удалось обойти все мосты по одному разу. Это не удалось даже самому великому Эйлеру, а он, наверно, был не худшим математиком, чем мы с вами. Эйлер однако установил следующие правила для того, чтобы заранее сказать, — можно ли обойти все мосты по одному разу. Обозначим отдельные местности, разделенные водой, (берега и острова) буквами А, В, С, Б и напишем таблицу, где в первом столбце будут названия местностей, во втором число мостов, соединяющихся с этой местностью. а в третьем столбце половины числа этих мостов, если они четные, и половины этих чисел, увеличенных на единицу, если он не четные. Затем складываем числа последнего столбца. Однократный полный обход мостов возможен только тогда, когда сумма эта равна числу мостов или больше его на единицу. Следует также заметить, что в первом случае (т. е. при равенстве суммы числу мостов) обход надо начинать с местностей, имеющих четное число мостов, а во втором случае — с местностей, где число мостов нечетное. Для Кенигсбергской задачи получим таблицу: