Д. Панков - Мир приключений, 1927 № 11

Храм божества Луны в Уре, по развалинам которого можно судить, что это было именно такое здание, как описывает впоследствии Навуходоносор, построен четырехугольником, с двойными стенами, в проходе между которыми помещалась стража. Храм был покрыт террасообразной крышей, к которой вели лестницы. Вокруг трех открытых дворов группировались алтари и различные помещения. Северный и южный дворы были священными местами, где ежедневно приносились жертвы. Один из этих дворов — самый лучший образец святилища, построенного за три столетия до Авраама. Бронзовые врата, закрывавшие его когда-то, исчезли, но дверные колонны уцелели до сих пор. На них надпись: «Царь Ур-Намму и царь Бур-Син, царь Ура, цари четырех стран земли». Места алтарей и водоемы сохранились вполне.

Подобно грекам, возведшим статую неведомого бога из страха, что они могли пренебречь каким-нибудь могущественным божеством, сумерийцы дружески относились к религиям других народов. Вокруг главного алтаря божества Луны находится множество ниш и боковых алтарей для статуй чужеземных богов и богинь. II действительно, единственная статуя, найденная неприкосновенной, это маленькая фигурка богини Бау, известная археологам как «Мать Гусыня», так как изображается обычно на волнах Евфрата в сопровождении двух гусей. Она не принадлежала к Уру, но была женой бога Иингирсу в Лагаше, за сорок миль от Ура.

В помещениях для склада запасов и в хранилищах драгоценностей находятся только ломаные камни и алавастровые сосуды. Много также каменных дощечек, покрытых надписями. В них говорится о далеких путешествиях и чудесных грузах, привезенных из разных стран. На одной дощечке описание морского путешествия, длившегося три года. Из этого путешествия вернулись со множеством золота, серебра, драгоценных камней и редкого дерева.

Раскопки льют все новый и новый свет на обычаи, описываемые в Библии. Там упоминается о том, что священнослужители посылали своих слуг с крючком о трех зубцах вылавливать для них мясо из жертвенного котла. Точно такой же обычай существовал в храмах божества Луны. В кухне при храме найден большой круглый котел, а перед ним площадка, на которую поднимались по лесенке слуги, чтобы достать оттуда долю жреца.

Задача № 64.

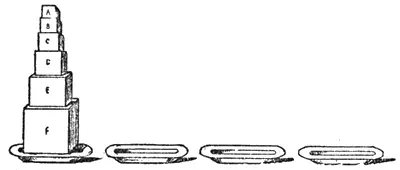
На одном из четырех блюд поставлены один на другом 6 уменьшающихся по размерам кубиков, А, В, С, Д, Е, F. Требуется все кубики в том же порядке, пользуясь запасными блюдами, установить на второе блюдо, соблюдая два правила: переносить кубики можно лишь по одному и не ставить больший над меньшим. Требуется определить наименьшее число и порядок необходимых перестановок (см. стр. 56).

Задача № 65.

Предыдущая задача не что иное, как упрощение одной индусской задачи. Задача эта настолько любопытна, что для ее решения стоит потратить немного времени. Вырезав из картона 8 небольших, постепенно уменьшающихся кружочков с отверстием посередине, надо взять кусок картона или небольшую дощечку и укрепить в ней три палочки высотой в несколько сантиметров (см. рис. внизу). Палочки эти обозначим буквами А, В, С. Наденем на палочку А наши картонные кружки, составив из них пирамиду. Теперь требуется с палочки А перенести всю пирамиду на палочку В. пользуясь, как вспомогательной, третьей палочкой С, при чем зараз можно переносить лишь один кружок и класть его или на свободную палочку, или на кружок большего размера. Вместо кружечков и палочек можно взять восемь карт, начиная от туза до восьмерки, и перекладывать их по одной, не закрывая меньшее число очков большим (см. стр. 56).

Задача № 66.

Начальник маленького железнодорожного полустанка получил телеграмму, что через короткое время проследует экстренный служебный поезд и чтобы были приняты меры к незамедлительному его пропуску. Но в это же время у полустанка на главном пути задержался товарный поезд. Кинулись переводить его на единственную запасную ветку, но, как на грех — ветка оказалась короче товарного поезда… Назад пустить его нельзя: — экстренный уже вышел, вперед — не успеет дойти до ближайшей станции и надолго задержит начальство… Тем не менее начальник полустанка нашелся и сумел пропустить экстренный поезд с самой ничтожной задержкой… Как он это сделал? (См. стр. 56).

Задача № 64.

Перенос кубика с блюда 1 на блюдо 2 можно сделать посредством 17 перемещении:

А на 2 В на 4 Е на 3 Д на 4 А на 1 В на 2

В па 3 А на 4 Д на 3 Е на 2 В на 3 А на 2

С на 4 Д на 2 F на 2 Д на 2 С на 2

Задача № 65.

Напишем табличку, где показан ход переложении, обозначая кружки цифрами, начиная сверху.　

Как общее правило, можно заметить, что на вспомогательную палочку С, когда она свободна, надеваются лишь нечетные кружки, а на В — при этом только четные. На перестановку двух кружков надо было сделать три переноса, для перестановки трех — семь переносов, для перестановки четырех — пятнадцать переносов, а вообще для перестановки и кружков надо совершить 2 n—1 переносов В нашей задаче с восемью кружками надо, таким образом, сделать 2 8—1, или 255 переносов.

В Индии существует легенда, будто в одном из храмов жрецы заняты переносом 64 золотых кружков, надетых на алмазные острия, и, когда все кружки будут переложены, наступит конец мира. Несомненно, жрецам придется поработать немало времени, т. к. при 64 кружках надо совершить двадцатизначное число перестановок. На это потребуется, считая по секунде на перестановку, пять слишком миллиардов веков.