И. Пименов - Мир приключений, 1928 № 08

В жеребьевке на последние премии принимали участив еще следующие лица: 11) Ф. Федоров (Минск); 12) С. И. Соколов (Москва); 13) В. И. Лапин (Новгород); 14) X. Файфман (Киев).

Задача № 13.

В напечатанном рисунке следует отметить, как «необычайное», следующие обстоятельства: 1) движение по левой стороне улиц, а не по правой; 2) стоянка одного автомобиля (второй слева) частично на тротуаре; 3) отсутствие «постового»; 4) отсутствие проводов (телеф., телегр.), фонарей, реклам, вывесок, тумб и водосточных труб у зданий; 5) сильное автомобильное движение при крайне слабом пешеходном; 6) распределение света (на здании слева) и теней (от машины и пешехода справа). — Если некоторые из этих обстоятельств вполне уместны в отношении к некоторым заграничным странам, то все-же совокупность их в одной картине представляет явление не только необычайное, но и неправдоподобное.

Комбинации из 5 спичек.

Задача № 14.

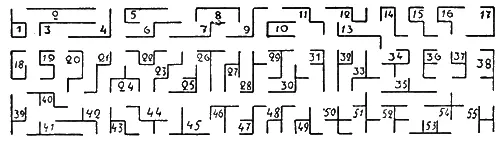
Все требуемые комбинации (выкладки) изображены на схеме, классифицированные по числу концов; 1 — с одним концом (1), 22 — с 2 концами (2-23). 26 — с 3 концами (24–49) и 6 — с 4 концами (50–55). Подбор по этому признаку, признаваемый нами наиболее простым, предложен лишь одним подписчиком (Соколов). Вполне годны и др. классификации: по числу прямых углов в фигурах (Смирнов, Каттербах и др.), по числу элементов (спичек), составляющих одну прямую линию (Федоров, Коломенский, Лапин и др.), по площади прямоугольного габарита (Княшко). Менее удачны системы с признаками по числу перегибов в местах соприкосновений (Виноградов), по «сторонностям» (Файфман), по симметричности или сходству (Тациевский). Правильный по математическому приему подход решения от всех комбинаций с меньшим числом элементов (с 2, 3 и 4 спичками) здесь оказывается сложнее других так как дает очень много повторений, трудно схватываемых анализом (так решали Кириллов-Губецкий, Лебедева).

Найдите число.

Задача № 15.

Алгебраически задача решается с помощью трех уравнений (с 3 неизвестными), формулирующих три заданных условия. При таком решении, совершенно простом алгебраически, из третьего заданного условия вытекает одно из свойств трехзначных обратных (вернее «обращенных») чисел: разность между ними, поделенная на 99, дает в частном разность между их крайними цифрами (в данном случае 594:99=6 ): иными словами, последняя разность (между крайними цифрами) составляет дополнение до 10 к последней цифре в разности между самими рассматриваемыми числами: в данное случае 6=10—4 (4 цифра единиц в 594).

Это свойство, легко доказуемое на примере и арифметически, является ключем к одному из арифметических решений. При разности между первой и последней цифрой искомого числа в 6 единиц, можно иметь для них выбор лишь в 4 возможностях: 9 и 3, 8 и 2, 7 и 1, 6 и 0. Но из второго условия задачи явствует, что обе крайние цифры не могут быть нечетными, п. ч. удвоенное произведение их должно делиться на 4 без остатка; значит из 4 возможностей остаются лишь две: 8 и 2, 6 и 0 . Этим случаям отвечают числа 862 и 620 (средние цифры находятся извлечением квадр. корня из 4+произведение крайних цифр). Вопрос решается окончательно в пользу первого числа — 852 — примеркой к первому условию задачи: (9×8)+(6×6)+(2×2) = 104.

Можно еще решить арифметически, исходя именно из первого условия, т. е. из последней приведенной формулы. Нетрудно убедиться, что число 104 нельзя разбить ни на какие иные 3 или 2 квадрата чисел (меньших 10 каждое), кроме приведенных выше цифр 8, 6 и 2. Расстановка этих трех цифр в искомое число легко делается при сопоставлении с 2-м и 4-м условиями задачи.

В оценке этой задачи, за всестороннее освещение ее, некоторым участникам конкурса было зачтено вместо 3 очков по 4.

Надо решить три помещенных здесь задачи №№ 21, 25 и 26. Качество решений оценивается очками, согласно указаний в заголовках самих задач. Еще полочка может быть прибавлено дополнительно за тщательность и аккуратность в выполнении решений, — при соблюдении, конечно, всех требуемых условий. Те участники конкурса, которые соберут в сумме наибольшее число очков, премируются следующими 10 премиями (при равенстве очков вопрос решается жребием):

1-я премия.«Лис Патрикеевич» — Гёте, большой том с 66 эстампами на меди и 21 гравюрами (ценность — 15 руб.).

2-я премия.Бесплатное получение в течение 1928 года журнала «Вестник Знания».

3-я премия. Грез — художественное издание с красочными иллюстрациями.

4-я премия. «Гений и творчество» — проф. Грузенберга — основы теории и психологии творчества.

5-я—10 премии. По выбору премированных одно из след. изданий: «Наука в вопросах и ответах», «Общественная медицина и социальная гигиена» — проф. З. Г. Френкель, «Пылающие бездны» — фантаст. роман Н. Муханова или шесть. №№ «Мир Приключений» за 1926 или 1927 г. г.

Все решения по конкурсу должны быть изложены на отдельном листе, сверху коего должны быть указаны фамилия, адрес и № подписного билета (или взамен того наклеен адрес с бандероли, под которой получается журнал). На конверте нужно делать надпись «В отдел задач».

Срок присылки решений — 25 октября с. г.

Трапеция с секретом.

Задача № 24 — до 4 очков.

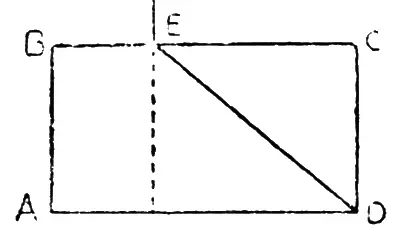
Возьмите любой прямоугольник, напр., ABCD (см. чертеж) и отрежьте от него уголок CED так, чтобы при подвеске оставшейся фигуры (трапеции ABED) на ниточке за точку Е основания этой трапеции AD и BE остались-бы перпендикулярными к отвесной нити. Второй вопрос: как изменится решение задачи, если взятый прямоугольник вытянуть или сжать по высоте его, сохранив прежнее основание ВС

Можно-ли угадать?

Задача № 25 — 2 очка.

Вам говорят, что задуманное число при делении на некоторый целый делитель дает частное А, а при делении на какой-то другой делитель дает частное В. Можно-ли и в каких именно случаях узнать задуманное число, если вам назовут оба частных А и Б?

Юбилейный акростих.

Задача № 26 — до 3 очков.

Подберите семь таких слов, которые при написании их столбцом одно под другим (буква под буквой) дадут прочесть в двух буквенных вертикалях, — с одной сверху вниз, а в другой снизу вверх, — фамилии двух классических русских писателей, юбилеи коих мы справляем в этом году. Подбираемые слова должны быть именами существительными нарицательными (в единств. числе, именит. падеже; и но возможности из одинакового числа букв.