Стивен Прата - Язык программирования C. Лекции и упражнения (6-е изд.) 2015

Метод дополнения до единицы формирует отрицательное число путем инвертирования каждого бита в комбинации. Например, комбинация 000000001 — это 1, а 11111110 — значение-1. Этот метод также имеет -0: 11111111. Диапазон представляемых чисел (для однобайтового значения) составляет от -127 до +127.

Двоичные числа с плавающей запятой

Числа с плавающей занятой хранятся в виде двух частей: двоичной дроби и двоичной экспоненты. Давайте посмотрим, как это происходит.

Двоичные дроби

Десятичная дробь 0.527 является следующей суммой:

5/10 + 2/100 + 7/1000

Здесь знаменатели представляют возрастающие степени 10. В двоичной дроби знаменатели будут степенями 2. Таким образом, двоичная дробь .101 может быть записана так:

1/2 + 0/4 + 1/8

В десятичной записи это имеет вид:

0.50 + 0.00 + 0.125 или 0.625.

Многие дроби, такие как 1 /3, не могут быть точно представлены в десятичной записи. Аналогично, многие дроби невозможно точно представить и в двоичной записи. На самом деле точно могут быть представлены лишь комбинации составляющих, которые кратны степеням 1/2. Таким образом, дроби 3/4 и 7/8 можно точно записать в двоичном представлении, но дроби 1/3 и 2/5 — нельзя.

Представление чисел с плавающей запятой

Представление числа с плавающей запятой в компьютере предусматривает выделение некоторого количества (в зависимости от системы) битов для хранения двоичной дроби. Дополнительные биты представляют экспоненту. В общих терминах действительное значение числа определяется как произведение двоичной дроби на 2 в степени, выраженной экспонентой. Умножение числа с плавающей запятой, скажем, на 4, увеличивает экспоненту в 2 раза, оставляя двоичную дробь неизменной. Умножение на число, не являющееся степенью 2, изменяет двоичную дробь и при необходимости экспоненту.

Манипулирование битами 631

Другие основания систем счисления

Специалисты в области компьютеров часто используют системы счисления с основаниями 8 и 16. Поскольку числа 8 и 16 являются степенями 2, эти системы счисления более тесно связаны с двоичной системой компьютера, чем десятичная система.

Восьмеричная система счисления

Восьмеричной называется система счисления с основанием 8. В этой системе каждое знакоместо в числе представляет степень 8. Для записи применяются цифры от 0 до 7. Например, восьмеричное число 451 (в С записывается как 0451) представлено следующим образом:

4 х 8 2+ 5 х 8 1+ 1 х 8 0= 297 (по основанию 10)

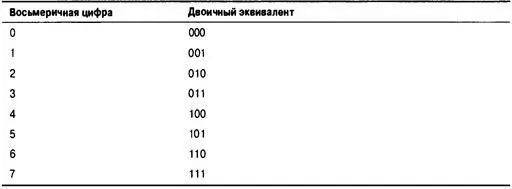
Каждая восьмеричная цифра соответствует трем двоичным цифрам (табл. 15.1). Такое соответствие упрощает перевод чисел между системами. Например, восьмеричное число 0377 — это двоичное число 11111111. Отбросив ведущий 0, мы заменяем 3 комбинацией 011, после чего каждую цифру 7 заменяем 111. Единственное неудобство состоит в том, что трехзначное восьмеричное число в двоичной форме может занимать до 9 битов. Поэтому восьмеричное значение, превышающее 0377, требует более одного байта. Обратите внимание, что внутренние нули не опускаются: числу 0173 соответствует комбинация 01 111 011, а не 01 111 11.

Таблица 15.1. Двоичные эквиваленты восьмеричных цифр

Шестнадцатеричная система счисления

Шестнадцатеричной называется система систему счисления с основанием 16. В ней используются степени 16 и цифры от 0 до 15, но из-за того, что в десятичной системе отсутствуют цифры для представления значений от 10 до 15, в шестнадцатеричной системе для них применяются буквы от А до Е Например, шестнадцатеричное число АЗЕ (в С записывается как 0xA3F) представляет следующее значение:

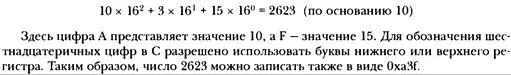
632 Глава 15

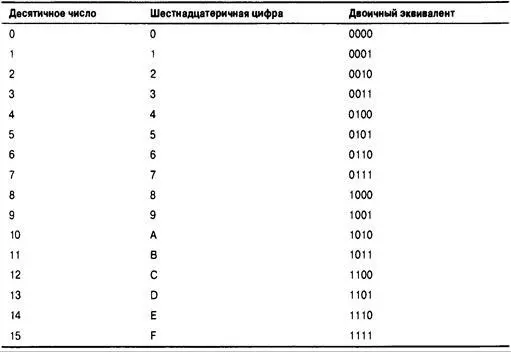
Каждая шестнадцатеричная цифра соответствует двоичному числу с 4 цифрами, так что две шестнадцатеричных цифры дают в точности один 8-битовый байт. Первая цифра представляет старшие 4 бита, а вторая цифра — младшие 4 бита. Это делает шестнадцатеричное представление естественным выбором для записи значений байтов. Соответствие между шестнадцатеричными цифрами и двоичными числами показано в табл. 15.2. Например, шестнадцатеричное число 0хС2 преобразуется в комбинацию 11000010. Для обратного преобразования комбинацию 11010101 необходимо представить в виде 1101 0101 и затем записать как 0xD5.

Таблица 15.2. Десятинные, шестнадцатеричные числа

и их двоичные эквиваленты

Теперь, когда вы ознакомились с понятием битов и байтов, давайте посмотрим, что в языке С можно с ними делать. Существуют два средства, помогающие манипулировать битами. Первое — это набор из шести побитовых операций, которые воздейству ют на биты. Второе средство — это форма полей данных, которая предоставляет доступ к битам внутри значения int. Эти средства обсуждаются в последующих разделах.

Побитовые операции

Язык С предлагает два вида побитовых операций: логические операции и операции сдвига. В последующих примерах мы будем записывать значения в двоичной системе, чтобы вы могли видеть, что происходит с битами. В действительной программе вы будете применять целочисленные переменные или константы в обычных формах. Например, вместо 00011001 будет использоваться запись 25, 031 или 0x19. В рассмат риваемых примерах мы будем применять 8-битовые числа с нумерацией битов слева направо от 0 до 7.

Манипулирование битами 633

побитовые логические операции

Четыре логических побитовых операции работают с целочисленными данными, включая тип char. Они называются побитовыми потому, что выполняются над каждым битом независимо от бита, находящегося слева или справа. Не путайте их с обычными логическими операциями (&&, || и !), которые имеют дело со значениями целиком.

Дополнение до единицы или побитовое отрицание: ~

Унарная операция ~ преобразует каждую единицу в ноль, а каждый ноль в единицу, как показано в следующем примере:

-(10011010) // выражение

(01100101) // результат

Предположим, что переменной val типа unsigned char присвоено значение 2. В двоичном виде 2 имеет вид 00000010. Тогда ~val будет иметь значение 11111101, или 253. Обратите внимание, что операция не изменяет значения переменной val, в точности как не изменяет значение val выражение 3 * val; значением val по-прежнему является 2, но создается новое значение, которое можно использовать или присваивать где-то в другом месте:

newval = -val; printf("%d", -val);

Если вы хотите изменить значение val на -val, применяйте следующий простой оператор присваивания:

val = -val;

Побитовая операция "И": &

Двоичная операция & создает новое значение за счет выполнения побитового сравнения двух операндов. Для каждой позиции результирующий бит будет равен 1, только если оба соответствующих бита в операндах равны 1. (В терминах истинный/ложный можно сказать, что результат будет истинным, только когда каждый из двух битовых операндов является истинным.) Таким образом, в результате вычисления выражения