Стивен Прата - Язык программирования C. Лекции и упражнения (6-е изд.) 2015

Библиотека математических функций

Библиотека математических функций содержит множество удобных функций такого рода. Их объявления или прототипы содержатся в заголовочном файле math.h. В табл. 16.2 перечислено несколько функций, объявленных в math.h. Обратите внимание, что все углы измеряются в радианах (один радиан составляет 180/Pi = 57.296 градуса). В разделе V приложения Б представлен полный список функций, определенных стандартом С99.

Таблица 16.2. Некоторые стандартные математические функции ANSI С

694 глава 16

Немного тригонометрии

Воспользуемся библиотекой математических функций для решения типичной задачи преобразования прямоугольных координат в полярные (модуль и угол). Предположим, что на сетке проведена линия, протяженность которой составляет 4 единицы по горизонтали (значение х) и 3 единицы по вертикали (значение у). Каковы длина (модуль) и направление линии? Согласно тригонометрии:

модуль = квадратный корень (х 2+ у 2)

и

угол = арктангенс (у/х)

Библиотека math предоставляет функцию извлечения квадратного корня и пару функций вычисления арктангенса, поэтому вы можете выразить данное решение на языке С. Функция извлечения квадратного корня, sqrt(), принимает аргумент double и возвращает квадратный корень аргумента также в виде значения double.

Функция atan() принимает аргумент double и возвращает угол, значение тангенса которого равно этому аргументу. К сожалению, функция atan() не учитывает квадрант вектора. Например, если координаты х и у вектора равны -5 и -5, функция atan() даст результат 45°, поскольку (-5)/(-5) = 1. Тот же результат будет для вектора с координатами 5 и 5. Другими словами, функция atan() не различает векторы, углы которых отличаются на 180°. (На самом деле функция atan() выводит результат в радианах, а не в градусах; мы обсудим это преобразование позже.)

К счастью, библиотека С содержит и функцию atan2(). Она принимает два аргумента: значения х и у. Таким образом, функция способна анализировать знаки коор дииат и правильно определять угол. Подобно atan() , функция atan2() возвращает угол в радианах.

Чтобы преобразовать радианы в градусы, умножьте результирующий угол на 180 и разделите на n. Вычисление значения га можно поручить компьютеру, указав выражение 4 * atan (1). Все описанные действия продемонстрированы в листинге 16.14. Вдобавок у вас есть шанс освежить в памяти знания структур и typedef.

Листинг 16.14. Программа rect_pol.c

Препроцессор и библиотека С 695

Ниже показаны результаты пробного запуска:

Введите координаты х и у; введите q для выхода:

10 10

модуль = 14.14, угол = 45.00 -12 -5

модуль = 13.00, угол = -157.38

q

Программа завершена.

Если в процессе компиляции будет выдано сообщение, такое как

Undefined: _sqrt Не определено: _sgrt

или

'sqrt': unresolved external

'sqrt': нераспознанный внешний идентификатор

либо нечто подобное, значит, компилятор-компоновщик не смог найти библиотеку математических функций. В системах Unix может потребоваться указать компоновщику на необходимость поиска библиотеки математических функций с помощью флага -1т:

сс rect_pol.с -1m

Обратите внимание, что флаг -1т находится в конце команды. Причина в том, что компоновщик вступает в игру после того, как компилятор скомпилирует файл С. Компилятор GC.C в системе Linux может вести себя в такой же манере:

gcc rect_pol.c -lm

Варианты типов

Базовые математические функции с плавающей запятой принимают аргументы типа double и возвращают значение типа double. Им можно передавать аргументы типа float или long double, и функции по-прежнему будут работать, поскольку аргументы указанных типов преобразуются в тип double. Это удобно, но не обязательно

696 Глава 16 оптимально. Если двойная точность не нужна, то вычисления могут выполняться быстрее, если применять значения float с одинарной точностью. К тому же значение типа long double будет терять точность при передаче параметру типа double; может даже оказаться, что значение вообще непредставимо. Чтобы решить такие потенциальные проблемы, в стандарте С предоставляются версии стандартных функций типа float и типа long double, имеющие в имени суффикс f или 1 (строчная буква T”). Таким образом, sqrtf() — это версия типа float функции sqrt(), a sqrtl() — версия типа long double функции sqrt().

Появление в С11 выражения обобщенного выбора позволяет определять обобщенный макрос, который выбирает наиболее подходящую версию математической функции на основе типа аргумента. В листинге 16.15 продемонстрированы два подхода.

Листинг 16.15. Программа generic.с

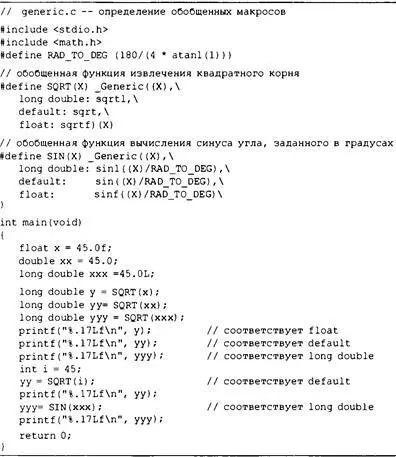
Вывод выглядит следующим образом:

6.70820379257202148

6.70820393249936942 6.70820393249936909

6.70820393249936942 0.70710678118654752

Препроцессор и библиотека С 697

Как видите, SQRT (i) имеет такое же возвращаемое значение, как у SQRT (хх), поскольку типы обоих аргументов (int и double) соответствуют метке default.

Интересно взглянуть на то, каким образом заставить макрос, использующий _Generic, действовать подобно функции. В определении SIN() предпринят, вероятно, наиболее очевидный подход: каждое помеченное значение представляет собой вызов функции, поэтому значением выражения _Generic является отдельный вызов функции, такой как sinf ( (X) /RAD_TO_DEG), с аргументом SIN(), заменяющим X.

Определение SQRT(), пожалуй, более элегантно. В этом случае значение выражения _Generic — это имя функции, такое как sinf. Это имя функции заменяется ее адресом, так что значением выражения _Generic будет указатель на функцию. Однако за полным выражением _Generic следует (X), и комбинация указатель-на- функцию (аргумент) вызывает указанную функцию с заданным аргументом.

Говоря кратко, для SIN() вызов функции находится внутри выражения обобщенного выбора, в то время как для SQRT() выражение обобщенного выбора оценивается как указатель, который затем применяется для вызова функции.

Библиотека tgmath.h (С99)

Стандарт С99 предлагает заголовочный файл tgmath.h, в котором определены макросы обобщенного типа, по своему действию похожие на те, что были показаны в листинге 16.15. Если какая-то функция matfi.li определена для каждого из трех типов float, double и long double, то файл tgmath.h создает макрос обобщенного типа с тем же именем, что и у версии для double. Например, он определяет макрос sqrt(), который разворачивается в функцию sqrtf(), sqrt() или sqrtl() в зависимости от типа предоставленного аргумента. Другими словами, макрос sqrt() ведет себя подобно макросу SQRT() из листинга 16.15.