Стивен Прата - Язык программирования C. Лекции и упражнения (6-е изд.) 2015

В листинге 5.6 представлен случай “смешанных типов”, когда значение с плавающей запятой делится на целое число. По сравнению с рядом других языков С более либерален и разрешает выполнять такие операции, однако обычно вы должны избегать смешивания типов. Ниже приведены результаты выполнения программы:

Целочисленное деление: 5/4 равно 1 Целочисленное деление: 6/3 равно 2 Целочисленное деление: 7/4 равно 1 Деление с плавающей запятой: 7./4. равно 1.75 Смешанное деление: 7./4 равно 1.75

Обратите внимание, что целочисленное деление не округляет до ближайшего целого, а всегда выполняет усечение (т.е. отбрасывает дробную часть). При смешивании водной операции целых чисел и чисел с плавающей запятой ответ оказывается таким же, как и в случае деления чисел с плавающей запятой. На самом деле компьютер не

Операции, выражения и операторы 167

способен делить число с плавающей запятой на целое число, и поэтому компилятор преобразует оба операнда к одному типу. В данном случае перед выполнением деления целое число преобразуется в число с плавающей занятой.

До появления стандарта С99 язык С предоставлял разработчикам реализаций некоторую свободу в решении того, как должно выполняться деление отрицательных чисел. Одна из точек зрения заключалась в том, что процедура округления предусматривает

нахождение наибольшего целого значения, которое меньше или равно числу с плавающей запятой. Естественно, число 3 удовлетворяет этому требованию, если его сравнивать с 3.8. Но как быть в случае -3.8? Метод нахождения наибольшего целого числа предполагает его округление до -4, поскольку -4 меньше, чем -3.8. Однако другая точка зрения на процесс округления состояла в том, что дробная часть просто отбрасывается; при такой интерпретации, называемой усечением в направлении нуля, предполагается преобразование числа -3.8 в -3. До выхода стандарта С99 в одних реализациях применялся первый подход, а в других — второй. Но в стандарте С99 определено усечение в направлении нуля, следовательно, -3.8 преобразуется в -3.

Свойства целочисленного деления оказываются очень удобными для решения некоторых задач, и вскоре вы ознакомитесь с примером. Сначала необходимо выяснить еще один важный аспект: что произойдет, если объединить несколько операций в один оператор? Это и является следующей темой.

приоритеты операций

Рассмотрим следующую строку кода:

butter =25.0+60.0 * n/ SCALE;

В этом операторе присутствуют операции сложения, умножения и деления. Какая из них выполнится первой? Будет ли 25.0 суммироваться с 60.0, полученный результат 85.0 умножаться на n, после чего произведение делиться на SCALE? Или же 60.0 умножится на n, к полученному произведению прибавится 2 5.0, после чего результат сложения разделится на SCALE? А, может быть, будет использоваться вообще другой порядок выполнения операции? Предположим, что n равно 6,0, a SCALE 2,0. При таких значениях первый подход даст результат 25 5, а второй — 192.5. По всей видимости, в программе на С задействован другой порядок, поскольку переменная butter в итоге получает значение 2 05.0.

Очевидно, что порядок выполнения различных операций оказывает влияние на конечный результат, следовательно, язык С нуждается в однозначных правилах выбора того, что должно выполняться в первую очередь. Эта проблема решается путем установки порядка выбора операций. Каждой операции назначается уровень приоритета. Как и в обычной арифметике, умножение и деление имеют более высокий приоритет, чем сложение и вычитание, поэтому они выполняются первыми. А что, если две операции обладают одинаковыми приоритетами? Когда они применяются к одному и тому же операнду, то выполняются в порядке следования внутри оператора. Большинство операций выполняются слева направо. (Операция = является исключением из этого правила.) Поэтому в операторе

butter =25.0+ 60.0 *n/ SCALE; операции выполняются в следующем порядке:

60.0 * n

Сначала выполняется первая операция * или / в выражении (при условии, что п равно 6, 60.0 * n дает 360.0).

360.0 / SCALE

168 Глава 5

Затем выполняется вторая операция * или / в выражении.

25.0 + 180

В завершение (поскольку SCALE равно 2.0) выполняется первая операция + в выражении, давая результат 205.0.

Многие люди предпочитают представлять порядок вычислений с помощью диаграммы, которая называется деревом выражения. Пример такой диаграммы продемонстрирован на рис. 5.3. Диаграмма показывает, как исходное выражение постепенно сводится к одному значению.

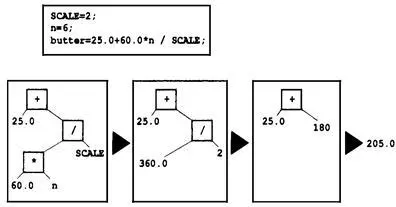
Рис. 5.1. Деревья выражений, показывающие операции, операнды и порядок вычиелтия

А что, если нужно обеспечить выполнение операции сложения раньше операции деления? Тогда можно поступить так, как это сделано в следующем операторе:

flour = (25.0 + 60.0 * n) / SCALE;

Все, что заключено в круглые скобки, выполняется первым. Внутри круглых скобок действуют обычные правила. В приведенном примере сначала выполняется умножение, а затем сложение. На этом вычисление выражения в круглых скобках завершено. Затем результат может быть разделен на SCALE.

Правила для рассмотренных операций обобщены в табл. 5.1.

Таблица 5.1. Операции в порядке снижения приоритета

Обратите внимание, что две формы использования знака “минус” имеют разные приоритеты, как и две формы применения знака “плюс”. В столбце “Ассоциативность” указано, как операция связывается с ее операндами. Например, унарная операция - ассоциируется с величиной, находящейся справа от нее, а в случае операции деления операнд слева делится на операнд справа.

Операции, выражения и операторы 169

приоритет и порядок вычисления

Приоритеты операций являются жизненно важным правилом для определения порядка вычисления выражения, но они не обязательно определяют полный порядок вычислений. Язык С оставляет определенную свободу выбора при реализации. Рассмотрим следующий оператор:

у = 6 * 12 + 5 * 20;

Приоритеты диктуют порядок вычисления, когда две операции применяются к одному операнду. Например, 12 является операндом для двух операций, * и +, и приоритет указывает, что умножение должно выполняться первым. Аналогично, согласно приоритетам, операнд 5 должен сначала умножаться, а не суммироваться. Короче говоря, операции умножения 6*12и5*20 выполняются до того, как начнет выполняться операция сложения. При этом приоритеты не устанавливают, какая из двух операций умножения выполняется первой. Язык С оставляет этот выбор за реализацией, поскольку один выбор может оказаться более эффективным для одного оборудования, а другой выбор обеспечивает более высокую производительность на другом оборудовании. В любом случае выражение сводится к 72 + 100, так что последовательность выполнения операций умножения в этом конкретном примере не оказывает влияния на окончательный результат. Однако у вас может возникнуть вопрос: поскольку умножение выполняется слева направо, не означает ли это, что самое левое умножение выполнится первым? Правило ассоциативности применяется к операциям, которые совместно используют операнд. Например, в выражении 12 / 3 * 2 операции / и *, обладающие одинаковыми приоритетами, совместно используют операнд 3. Таким образом, в этом случае применяется правило “слева направо”, и выражение сводится к 4 * 2, т.е. 8. (Выполнение справа налево привело бы к 12 / 6, или 2. В этом случае выбор имеет значение.) В предыдущем примере две операции * не имеют общего операнда, так что правило “слева направо” не применяется.