Эндрю Уэзеролл - Компьютерные сети. 5-е издание

Увеличить количество информации, которое необходимо передавать (чтобы скорость составила b бит/с, нужно отправлять mb элементарных сигналов в секунду), можно только за счет увеличения в m раз пропускной способности. Таким образом, для CDMA нужна в m раз большая пропускная способность, чем для станции не

применяющей CDMA (предполагая, что никаких изменений в методах модуляции и кодирования не производилось). Если имеется полоса шириной 1 МГц, на которой работают 100 станций, то при частотном уплотнении каждая из них получила бы свои 10 кГц и работала бы со скоростью 10 Кбит/с (предположим, используется 1 бит/Гц). При CDMA каждая станция использует всю ширину диапазона (1 МГц), так что скорость передачи элементарных сигналов достигает сотни и «размазывает» пропускную способность станции 10 Кбит/с на все каналы.

На рис. 2.24, а и б мы покажем элементарные последовательности четырех станций и сигналы, которыми они представляются.

Каждая станция имеет собственную уникальную элементарную последовательность. Обозначим символом S вектор длины m для станции S, а символом S — дополнение S. Все элементарные последовательности попарно ортогональны. Мы имеем в виду, что нормированное скалярное произведение двух различных элементарных последовательностей S и T (пишется S • T ) равно 0. Известно, как генерировать такие последовательности с помощью метода, известного как коды Уолша. Используя математическую запись, можно выразить вышесказанное таким образом:

Попросту говоря, сколько всего пар, столько и разных пар. Это свойство ортогональности мы строго докажем чуть позже. Обратите внимание: если S • T = 0, то и S • T также равно 0. Нормированное скалярное произведение любой элементарной последовательности на саму себя равно 1:

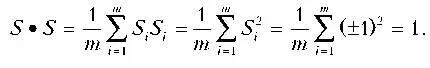
Это действительно так, поскольку каждое из m слагаемых суммы равно 1, поэтому вся сумма равна m. Обратите также внимание на то, что S • S = -1.

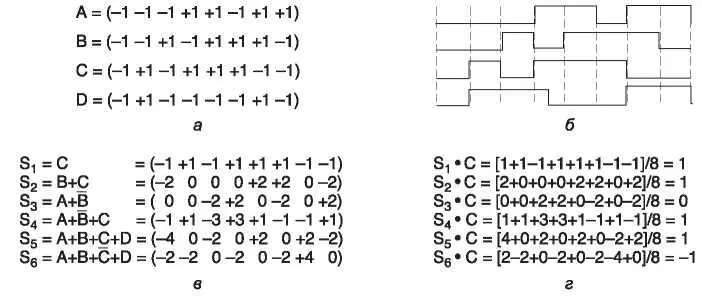
Рис. 2.24.Последовательность: а — двоичные элементарные последовательности для четырех станций; б — биполярные элементарные двоичные последовательности; в — шесть примеров передачи; г — восстановление сигнала станции C

В течение каждого битового интервала станция может либо передавать 1, посылая свою элементарную последовательность, либо передавать 0, посылая дополнение к последовательности, либо может молчать и ничего не передавать. Предположим, что все станции синхронизировались во времени, то есть все последовательности начали передаваться в один и тот же момент.

Когда две или более станции пытаются осуществить одновременную передачу, их биполярные сигналы линейно складываются. Например, если при передаче одного элементарного сигнала три станции послали +1, а одна послала -1, то в результате получится +2. Можно рассматривать это как сложение напряжений: три станции имеют на выходе +1 В, а одна имеет на выходе -1 В. В результате сложения получаем +2 В.

На рис. 2.24, в изображено шесть примеров передачи, в которой одновременно принимают участие одна или несколько станций. В первом примере С передает единичный бит, поэтому мы просто получаем элементарную последовательность этой станции. Во втором примере и B и C передают единичные биты, в результате чего мы получаем сумму их биполярных последовательностей, а именно:

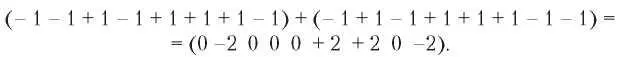
(- 1 - 1 + 1 - 1 + 1 + 1 + 1 - 1) + (- 1 + 1 - 1 + 1 + 1 + 1 - 1 - 1) =

= (0 -2 000 + 2 + 2 0 -2).

Чтобы восстановить исходный битовый поток каждой из станций, приемник должен заранее знать элементарные последовательности всех передатчиков, с которыми он работает. Восстановление осуществляется путем вычисления нормированного скалярного произведения принятой последовательности (то есть линейной суммы сигналов всех станций) и элементарной последовательности той станции, чей исходный сигнал восстанавливается. Если принята элементарная последовательность S и приемник пытается понять, что передала станция с элементарной последовательностью C , то производится вычисление нормированного скалярного произведения S • C.

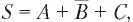
Чтобы понять, как это все работает, давайте представим себе эти две станции, A и C. Пусть обе передают единичный бит в то время, как станция B передает нулевой бит. Приемник получает сумму сигналов, которая равна: S = A + B + C, и вычисляет произведение:

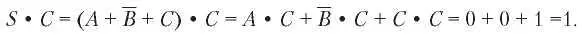
S • C = (A + B + C) • C = A • C + B • C + C • C = 0 + 0 + 1 =1.

Первые два слагаемых равны нулю, потому что все пары элементарных последовательностей тщательно подбирались такими, чтобы они были ортогональными, см. выражение (2.3). Теперь понятно, почему это условие должно быть наложено на элементарные последовательности.

Обратимся снова к шести примерам, показанным на рис. 2.24, в. Конкретный результат декодирования этих последовательностей представлен на рис. 2.24, г. Допустим, приемник заинтересован в извлечении потока битов, посланного станцией C , из всех шести последовательностей S 1-S 6. Для этого он вычисляет каждый бит путем суммирования парных произведений принятой последовательности ( S ) и вектора C (см. рис. 2.24, б), затем деления результата на 8 (так как m = 8 в данном случае). Как видите, каждый раз находится верный бит. Это так же просто, как говорить по-французски!

В идеальной системе CDMA без учета шумов, которую мы здесь изучили, допустимое количество станций, которые передают сигналы одновременно, может быть сколь угодно большим, при этом будут использоваться более длинные последовательности чипов. Для 2 п станции коды Уолша могут обеспечить 2 п ортогональных последовательностей длины 2 п. Однако имеется одно существенное ограничение — то, что мы предположили, что все чипы синхронизированы по времени в приемнике. Эта синхронизация даже приближенно не выполняется в таких приложениях, как сотовая связь (где CDMA был широко внедрен начиная с 1990-х).

Мы вернемся к этой теме позже и опишем, чем асинхронный CDMA отличается от синхронного CDMA.