Эндрю Уэзеролл - Компьютерные сети. 5-е издание
- Название:Компьютерные сети. 5-е издание
- Автор:
- Жанр:
- Издательство:Питер
- Год:2011
- ISBN:9785446100682
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эндрю Уэзеролл - Компьютерные сети. 5-е издание краткое содержание
Компьютерные сети. 5-е издание - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Однако можно сделать кое-что еще, чтобы повысить уровень защиты от последовательностей ошибок — биты четности можно вычислять в порядке, отличном от того, в котором данные отправляются. Этот способ называется чередованием( interleaving). В нашем примере мы будет вычислять бит четности для каждого из n столбцов, но биты данных отправляться будут в виде k строк, в обычном порядке: сверху вниз и слева направо. В последней строке отправим n бит четности. На рис. 3.8 порядок пересылки показан для n = 7 и k = 7.
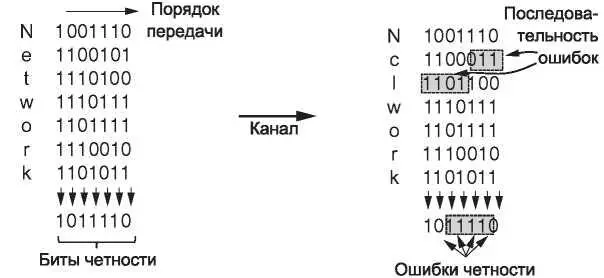
Рис. 3.8.Чередование битов четности для обнаружения последовательностей ошибок
Чередование представляет собой общую технику преобразования кода, способного обнаруживать (или исправлять) изолированные ошибки, в код, обнаруживающий (или исправляющий) последовательности ошибок. На рис. 3.8, там, где присутствует последовательность ошибок длиной n = 7, мы видим, что ошибочные биты находятся в разных столбцах (последовательность ошибок не означает, что все биты в ней неправильные; это всего лишь подразумевает, что, по меньшей мере, первый и последний биты сбойные. На рис. 3.8 из семи сбойных бит на самом деле изменено значение только четырех). В каждом из n столбцов повреждено будет не больше одного бита, поэтому биты четности этих столбцов помогут выявить ошибку. В данном методе n бит четности в блоках из kn битов данных применяются для обнаружения одной последовательности ошибок длиной n бит или меньше.
Последовательность ошибок длиной n + 1 не будет обнаружена, если будут инвертированы первый и последний биты, а все остальные биты останутся неизменными. Если в блоке при передаче возникнет длинная последовательность ошибок или несколько коротких, вероятность того, что четность любого из n столбцов будет верной (или неверной), равна 0,5, поэтому вероятность необнаружения ошибки будет равна 2 -n.
Второй тип кода с обнаружением ошибок, код с использованием контрольной суммы, весьма напоминает группу кодов, применяющих биты четности. Под «контрольной суммой» часто подразумевают любую группу контрольных бит, связанных с сообщением, независимо от способа их вычисления. Группа бит четности — также один из примеров контрольной суммы. Однако существуют и другие, более надежные контрольные суммы, основанные на текущей сумме бит данных в сообщении. Контрольная сумма обычно помещается в конец сообщения, в качестве дополнения функции суммирования. Таким образом, ошибки можно обнаружить путем суммирования всего полученного кодового слова: бит данных и контрольной суммы. Если результат равен нулю, значит, ошибок нет.
Один из примеров контрольной суммы — это 16-битная контрольная сумма, которая используется во всех пакетах протокола IP при пересылке данных в Интернете (Braden и др., 1988). Она представляет собой сумму бит сообщения, поделенного на 16-битные слова. Так как данный метод работает со словами, а не с битами (как при использовании битов четности), то ошибки, при которых четность не меняется, все же изменяют значение суммы, а значит, могут быть обнаружены. Например, если бит младшего разряда в двух разных словах меняется с 0 на 1, то проверка четности этих битов не выявит ошибку. Однако при добавлении к 16-битной контрольной сумме две единицы дадут другой результат, и ошибка станет очевидной.
Контрольная сумма, применяемая в Интернете, вычисляется с помощью обратного кода или арифметики с дополнением до единицы, а не как сумма по модулю 2 16. В арифметике обратного кода отрицательное число представляет собой поразрядное дополнение своего положительного эквивалента. Большинство современных компьютеров работают на арифметике с дополнением до двух, в которой отрицательное число является дополнением до единицы плюс один. На компьютере с арифметикой с дополнением до двух сумма с дополнением до единицы эквивалентна сумме по модулю 2 16, причем любое переполнение старших бит добавляется обратно к младшим битам. Такой алгоритм обеспечивает единообразный охват данных битами контроль
ной суммы. В противном случае при сложении двух старших бит переполнение может быть утеряно без изменения суммы. Но есть и еще одно преимущество. У дополнения до единицы может быть два представления нуля: все нули и все единицы. Таким образом, одно значение (например, все нули) указывает, что контрольной суммы нет и дополнительное поле для этого не требуется.
Десятилетиями существовало мнение, что кадры, для которых вычисляется контрольная сумма, содержат случайные значения бит. Анализ алгоритмов вычисления контрольных сумм всегда проводился с учетом именно такого предположения. Изучение фактических данных, выполненное Партриджем и другими в 1995 году, показало, что данное предположение неверно. Следовательно, нераспознанные ошибки проскальзывают в некоторых случаях намного чаще, чем полагали раньше.
В частности, контрольная сумма для Интернета, несмотря на эффективность и простоту, в определенных ситуациях слабо защищает от ошибок именно потому, что это простая сумма. Она не позволяет распознать удаление или добавление нулевых данных, а также случаи, когда части сообщения меняются местами или расщепляются таким образом, что склеенными оказываются части двух разных пакетов. Может казаться, что подобные ошибки вряд ли произойдут в случайных процессах, но они вполне вероятны в сетях с неправильно работающим оборудованием.
Намного лучшим выбором считается контрольная сумма Флетчера (Fletcher, 1982). Она включает компонент, отвечающий за позицию: произведение значения данных и соответствующей позиции добавляется к текущей сумме. Это обеспечивает лучшие возможности по обнаружению изменений в положении данных.
Хотя две приведенные выше схемы в некоторых случаях могут быть приемлемыми на более высоких уровнях, на практике на канальном уровне широко используется другой, более надежный метод обнаружения ошибок — полиномиальный код, так же известный, как CRC (Cyclic Redundancy Check — циклический избыточный код).

С данными многочленами осуществляются арифметические действия по модулю 2 в соответствии с алгебраической теорией поля. При этом перенос при сложении и заем при вычитании не производится. И сложение, и вычитание эквивалентны исключающему ИЛИ (XOR).
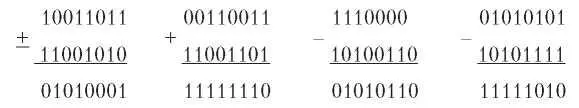
Интервал:
Закладка:








