Педро Домингос - Верховный алгоритм

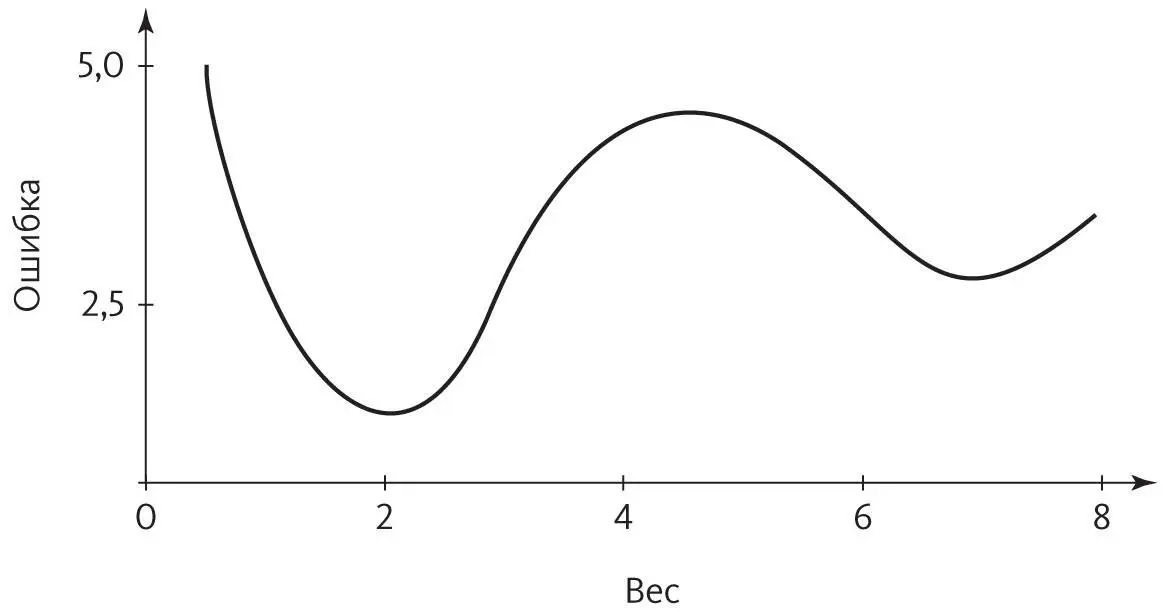
Оптимальный вес, в котором ошибка самая низкая, — это 2,0. Если сеть начнет работу, например, с 0,75, обратное распространение ошибки за несколько шагов придет к оптимуму, как катящийся с горки мячик. Однако если начать с 5,5, мы скатимся к весу 7,0 и застрянем там. Обратное распространение ошибки со своими поэтапными изменениями весов не сможет найти глобальный минимум ошибки, а локальные минимумы могут быть сколь угодно плохими: например, бабушку можно перепутать со шляпой. Если вес всего один, можно перепробовать все возможные значения c шагом 0,01 и таким образом найти оптимум. Но когда весов тысячи, не говоря уже о миллионах или миллиардах, это не вариант, потому что число точек на сетке будет увеличиваться экспоненциально с числом весов. Глобальный минимум окажется скрыт где-то в бездонных глубинах гиперпространства — ищи иголку в стоге сена.

Представьте, что вас похитили, завязали глаза и бросили где-то в Гималаях. Голова раскалывается, с памятью не очень, но вы твердо знаете, что надо забраться на вершину Эвереста. Как быть? Вы делаете шаг вперед и едва не скатываетесь в ущелье. Переведя дух, вы решаете действовать систематичнее и осторожно ощупываете ногой почву вокруг, чтобы определить самую высокую точку. Затем вы робко шагаете к ней, и все повторяется. Понемногу вы забираетесь все выше и выше. Через какое-то время любой шаг начинает вести вниз, и вы останавливаетесь. Это градиентное восхождение. Если бы в Гималаях существовал один Эверест, причем идеальной конической формы, все было бы прекрасно. Но, скорее всего, место, где все шаги ведут вниз, будет все еще очень далеко от вершины: вы просто застрянете на каком-нибудь холме у подножья. Именно это происходит с обратным распространением ошибки, только на горы оно взбирается в гиперпространстве, а не в трехмерном пространстве, как наше. Если ваша сеть состоит из одного нейрона и вы будете шаг за шагом подниматься к наилучшим весам, то придете к вершине. Но в многослойном перцептроне ландшафт очень изрезанный — поди найди высочайший пик.

Отчасти поэтому Минский, Пейперт и другие исследователи не пони­мали, как можно обучать многослойные перцептроны. Они могли представить себе замену ступенчатых функций S-образными кривыми и градиентный спуск, но затем сталкивались с проблемой локальных минимумов ошибки. В то время ученые не доверяли компьютерным симуляциям и требовали математических доказательств работо­способности алгоритма, а для обратного распространения ошибки такого доказательства не было. Но, как мы уже видели, в большинстве случаев локального минимума достаточно. Поверхность ошибки часто похожа на дикобраза: много крутых пиков и впадин, и на самом деле неважно, найдем ли мы самую глубокую, абсолютную впадину — сойдет любая. Еще лучше то, что локальный минимум бывает даже предпочтительнее, потому что он меньше подвержен переобучению, чем глобальный.

Гиперпространство — обоюдоострый меч. С одной стороны, чем больше количество измерений, тем больше места для очень сложных поверхностей и локальных экстремумов. С другой стороны, чтобы застрять в локальном экстремуме, надо застрять во всех измерениях, а во многих одновременно застрять сложнее, чем в трех. В гиперпространстве есть перевалы, проходящие через всю (гипер)местность, поэтому с небольшой помощью со стороны человека обратное распространение ошибки зачастую способно найти путь к идеально хорошему набору весов. Может быть, это не уровень моря, а только легендарная долина Шангри-Ла, но на что жаловаться, если в гиперпространстве миллионы таких долин и к каждой ведут миллиарды перевалов?

Тем не менее придавать слишком большое значение весам, которые находит обратное распространение ошибки, не стоит. Помните, что есть, вероятно, много очень разных, но одинаково хороших вариантов. Обучение многослойного перцептрона хаотично в том смысле, что, начав из слегка отличающихся мест, он может привести к весьма различным решениям. Этот феномен проявляется в случае незначительных отличий как в исходных весах, так и в обучающих данных и имеет место во всех мощных обучающихся алгоритмах, а не только в обратном распространении ошибки.

Мы могли бы избавиться от проблемы локальных экстремумов, убрав наши сигмоиды и позволив каждому нейрону просто выдавать взвешенную сумму своих входов. Поверхность ошибки стала бы в этом случае очень гладкой, и остался бы всего один минимум — глобальный. Дело, однако, в том, что линейная функция линейных функций — по-прежнему линейная функция, поэтому сеть линейных нейронов ничем не лучше, чем единичный нейрон. Линейный мозг, каким бы большим он ни был, будет глупее червяка. S-образные кривые — просто хороший перевалочный пункт между глупостью линейных функций и сложностью ступенчатых функций.

Перцептроны наносят ответный удар

Метод обратного распространения ошибки был изобретен в 1986 году Дэвидом Румельхартом, психологом из Калифорнийского университета в Сан-Диего, в сотрудничестве с Джеффом Хинтоном и Рональдом Уильямсом66. Они доказали, кроме всего прочего, что обратное распространение способно справиться с исключающим ИЛИ, и тем самым дали коннекционистам возможность показать язык Минскому и Пейперту. Вспомните пример с кроссовками Nike: подростки и женщины среднего возраста — их наиболее вероятные покупатели. Это можно представить с помощью сети из трех нейронов: один срабатывает, когда видит подростка, другой — женщину среднего возраста, а третий — когда активизируются оба. Благодаря обратному распространению ошибки можно узнать соответствующие веса и получить успешный детектор предполагаемых покупателей Nike. (Вот так-то, Марвин.)

В первых демонстрациях мощи обратного распространения Терри Сейновски и Чарльз Розенберг обучали многослойный перцептрон читать вслух. Их система NETtalk сканировала текст, подбирала фонемы согласно контексту и передавала их в синтезатор речи. NETtalk не только делал правильные обобщения для новых слов, чего не умели системы, основанные на знаниях, но и научился говорить очень похоже на человека. Сейновски любил очаровывать публику на научных мероприятиях, пуская запись обучения NETtalk: сначала лепет, затем что-то более внятное и наконец вполне гладкая речь с отдельными ошибками. (Поищите примеры на YouTube по запросу sejnowski nettalk.)

Первым большим успехом нейронных сетей стало прогнозирование на фондовой бирже. Поскольку сети умеют выявлять маленькие нелинейности в очень зашумленных данных, они приобрели популярность и вытеснили распространенные в финансах линейные модели. Типичный инвестиционный фонд тренирует сети для каждой из многочисленных ценных бумаг, затем позволяет выбрать самые многообещающие, после чего люди-аналитики решают, в какую из них инвестировать. Однако ряд фондов пошел до конца и разрешил алгоритмам машинного обучения осуществлять покупки и продажи самостоятельно. Сколько именно из них преуспело — тайна за семью печатями, но, поскольку специалисты по обучающимся алгоритмам в устрашающем темпе исчезают в недрах хеджевых фондов, вероятно, в этом что-то есть.