Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]
- Название:Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]
- Автор:
- Жанр:
- Издательство:Олимп-Бизнес
- Год:2009
- Город:Москва
- ISBN:978-5-9693-0163-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе] краткое содержание
Дуглас Хаббард пытается развеять это вредное заблуждение, предлагая свой подход к оценке «неизмеряемого», названный им «прикладная информационная экономика». Он знакомит читателей с понятием «калиброванная оценка», оценкой риска (метод Монте-Карло), способами выборочного исследования, другими необычными инструментами измерений (Интернет, экспертные оценки, рынки предсказаний и др.), а также с оценкой стоимости информации. Свой подход автор применяет в разных областях и приводит ряд примеров успешного решения задач по количественному измерению. В книге содержатся ценные инструкции и рекомендации, которые без труда может использовать любой человек, принимающий решения, а также приложения, позволяющие проверить способность читателя давать калиброванные оценки.
Книга предназначена широкому кругу читателей, интересующихся процессами обоснования и принятия решений. Она будет полезна руководителям, менеджерам, преподавателям и студентам.
Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе] - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
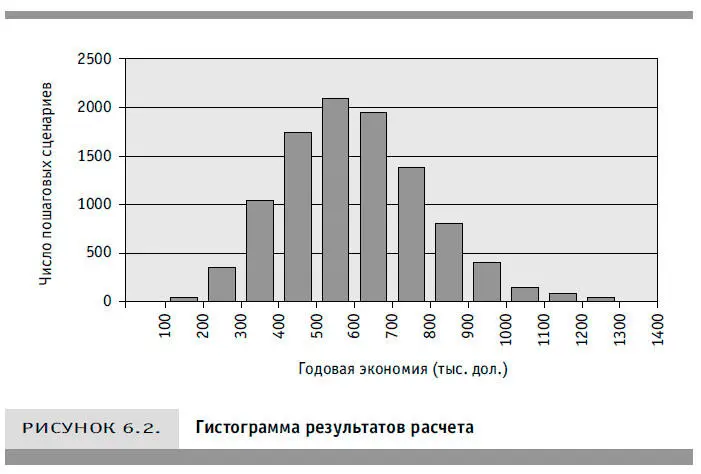
Из всех полученных значений годовой экономии примерно 14 % будут меньше 400 000 дол. Это означает, что вероятность ущерба составляет 14 %. Данное число и представляет содержательную оценку риска. Но риск не всегда сводится к возможности отрицательной доходности инвестиций. Оценивая размеры вещи, мы определяем ее высоту, массу, обхват и т. д. Точно так же существуют и несколько полезных показателей риска. Дальнейший анализ показывает: есть вероятность 3,5 % того, что завод вместо экономии будет терять ежегодно по 100 млн дол. Однако полное отсутствие доходов практически исключено. Вот что подразумевается под анализом риска — мы должны уметь рассчитывать вероятности ущерба разного масштаба. Если вы действительно измеряете риск, то должны делать именно это. С дополнительным материалом к данному примеру можно ознакомиться на сайте www.howtomeasureanything.com
В некоторых ситуациях можно пойти более коротким путем. Если все распределения значений, с которыми мы работаем, будут нормальными и нам надо просто сложить интервалы этих значений (например, интервалы затрат и выгод) или вычесть их друг из друга, то можно обойтись и без моделирования методом Монте-Карло. Когда необходимо суммировать три вида экономии из нашего примера, следует провести простой расчет. Чтобы получить искомый интервал, используйте шесть шагов, перечисленных ниже:
1) произвести вычитание среднего значения каждого интервала значений из его верхней границы. Для экономии на материально-техническом обслуживании — 20–15 = 5 (дол.), для экономии на трудозатратах — 5 дол. и для экономии на сырье и материалах — 3 дол.;
2) возвести в квадрат результаты первого шага — 5 2= 25 (дол.) и т. д.;
3) суммировать результаты второго шага — 25 + 25 + 9 = 59 (дол.);
4) извлечь квадратный корень из полученной суммы (получится 7,68 дол.);
5) сложить все средние значения: 15 + 3 + 6 = 24 (дол.);
6) прибавить к сумме средних значений или вычесть из нее результат шага 4 и получить в итоге верхнюю и нижнюю границы диапазона: 24 + 7,68 = 31,68 (дол.) — верхняя граница; 24–7,68 = 16,32 (дол.) — нижняя граница.
Таким образом, 90-процентный доверительный интервал для суммы трех 90-процентных доверительных интервалов по каждому виду экономии составляет 16,32–31,68 дол. В итоге область значений (размах) суммарного интервала равна квадратному корню из суммы квадратов областей значений отдельных интервалов.
Иногда нечто похожее делают, суммируя все «оптимистические» значения верхней границы и «пессимистические» значения нижней границы интервала. В данном случае мы получили бы на основе наших трех 90-процентных доверительных интервалов суммарный интервал 11–37 дол. Этот интервал несколько шире, чем 16,32–31,68 дол. Когда такие расчеты выполняются при обосновании проекта с десятками переменных, расширение интервала становится чрезмерным, чтобы его игнорировать. Брать самые «оптимистические» значения для верхней границы и «пессимистические» для нижней — все равно что думать: бросив несколько игральных костей, мы во всех случаях получим только «1» или только «6». На самом же деле выпадет некое сочетание низких и высоких значений. Чрезмерное расширение интервала — распространенная ошибка, которая, несомненно, часто приводит к принятию необоснованных решений. В то же время описанный мной простой метод прекрасно работает, когда у нас есть несколько 90-процентных доверительных интервалов, которые необходимо суммировать.
Однако наша цель не только суммировать интервалы, но и умножить их на объем производства, значения которого также даны в виде диапазона. Простой метод суммирования годится только для вычитания или сложения интервалов значений.
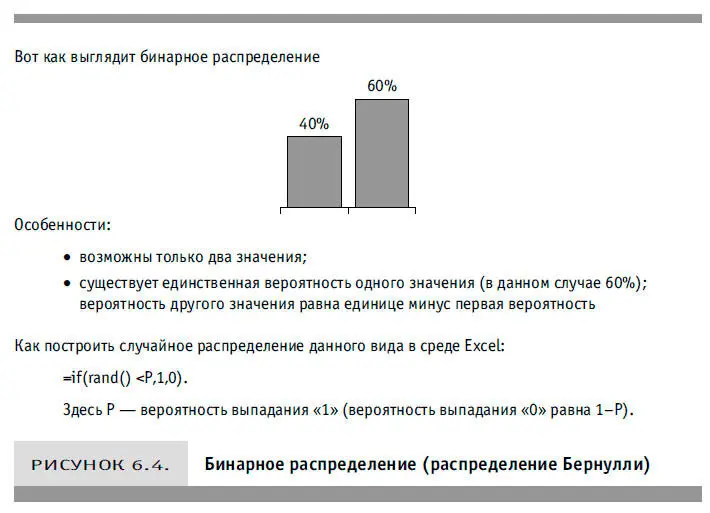
Моделирование методом Монте-Карло требуется и тогда, когда не все распределения являются нормальными. Хотя другие типы распределений не входят в предмет данной книги, упомянем о двух из них — равномерном и бинарном (см. рис. 6.3 и 6.4). И то и другое нам еще встретится, когда мы будем обсуждать стоимость информации.

Инструменты и другие ресурсы для моделирования методом Монте-Карло
К счастью, сегодня вам не придется строить модель Монте-Карло с нуля. Существуют многочисленные инструменты, облегчающие труд знакомого с теорией аналитика и повышающие его эффективность. К ним относятся и простые наборы макросов для Excel (которыми пользуюсь я), и очень сложные пакеты программ.
Горячим сторонником использования метода Монте-Карло в бизнесе является профессор Стэнфордского университета Сэм Сэвидж, разработавший инструмент, названный им Insight.xls. Сэвидж предлагает интуитивный подход к использованию вероятностного анализа. Кроме того, у него есть кое-какие соображения по поводу формализации процедуры разработки моделей методом Монте-Карло. Если такими моделями пользуются разные подразделения одной и той же организации, то, по мнению Сэвиджа, ей следует иметь объединенную базу общих распределений, а не придумывать каждый раз новые распределения для одних и тех же величин. Более того, он считает, что само определение распределения величины часто представляет собой особую задачу, требующую некоторой математической подготовки.
У Сэвиджа есть интересный метод, который он называет управлением вероятностями: «Предположим, описание распределений вероятностей мы возьмем на себя. Чем тогда вы сможете оправдать свое нежелание пользоваться распределениями вероятностей? Некоторые говорят, что не умеют описывать распределение вероятностей. Однако как выработать электроэнергию, они тоже не знают, но все же ею пользуются».
Его идея заключается в том, чтобы ввести в компаниях такую должность, как ведущий специалист по вероятностям. Он будет отвечать за управление объединенной библиотекой распределений вероятностей, которой может пользоваться каждый, кто занимается моделированием по методу Монте-Карло. Сэвидж ввел такое понятие, как стохастический информационный пакет (stochastic information packet, SIP) — заранее разработанный набор из 100 000 случайных значений того или иного показателя. Иногда разные пакеты связаны друг с другом. Например, доход компании может согласовываться с темпами роста национальной экономики. Набор таких коррелирующих между собой стохастических информационных пакетов называется стохастическими библиотечными модулями с сохраненными зависимостями (stochastic library units with relationships preserved, SLURPs). Ведущий специалист по вероятностям будет управлять SIP и SLURPs таким образом, чтобы пользователям распределений вероятностей не приходилось изобретать велосипед всякий раз, когда нужно моделировать инфляцию или затраты на здравоохранение.
Читать дальшеИнтервал:
Закладка:
![Обложка книги Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]](/books/1063946/duglas-habbard-kak-izmerit-vse-chto-ugodno-ocenk.webp)









