Лидия Щербина - Общая теория статистики

Между признаками выборочной совокупности и признаками генеральной совокупности существует некоторое расхождение, которое называют ошибкой статистического наблюдения. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности.

Под ошибкой репрезентативности (представи–тельства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентатив–ности бывают случайными и систематическими.

Систематические ошибки связаны с нарушени–ем установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности раз–личных категорий единиц генеральной совокупно–сти. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда напра–вленная в одну и ту же сторону. Эта ошибка получи–ла название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особен–ность ошибки смещения состоит в том, что, пред–ставляя собой постоянную часть ошибки репре–зентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличени–ем объема выборки уменьшается.

Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной сово–купности.

Случайная ошибка выборки возникает в результа–те случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.

Предельные теоремы теории вероятностей по–зволяют определять размер случайных ошибок вы–борки. Различают среднюю (стандартную) и предель–ную ошибки выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностями. Предельной ошибкой выборки принято считать мак–симально возможное расхождение.

В математической теории выборочного метода сравниваются средние характеристики признаков вы–борочной и генеральной совокупностей и доказывает–ся, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются.

Интервал, в который с данной степенью вероят–ности будет заключена неизвестная величина оцени–ваемого параметра, называют доверительным, а ве–роятность Р – доверительной вероятностью.

Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответ–ствующей характеристике выборочной совокупности.

Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в ге–неральной совокупности.

Одним из научных принципов в теории выбороч–ного метода является обеспечение достаточного чи–сла отобранных единиц.

Уменьшение стандартной ошибки выборки всег–да связано с увеличением объема выборки. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки ( Δ ) , соответствующих тому или иному ви–ду и способу отбора. Так, для случайного повторного объема выборки (n) имеем:

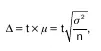
откуда

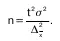
При случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия и дисперсии вариа–ционного признака и обратно пропорционален ква–драту предельной ошибки выборки. В частности, с увеличением предельной ошибки в 2 раза необхо–димая численность выборки может быть уменьшена в 4 раза. Из трех параметров два (коэффициент дове–рия и предельная ошибка выборке) задаются иссле–дователем. При этом исследователь исходя из цели и задач выборочного обследования должен решить вопрос, в каком количественном сочетании луч–ше включить эти параметры для обеспечения оп–тимального варианта. В одном случае его может устраивать в большей мере надежность полученных ре–зультатов (t), нежели мера точности ( Д ), в другом – наоборот. Сложнее решить вопрос в отношении вели–чины предельной ошибки выборки, так как этим пока–зателем исследователь на стадии проектировки вы–борочного наблюдения не располагает. В практике принято задавать величину предельной ошибки вы–борки в пределах до 10% предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по-разному: ис–пользовать данные подобных ранее проведенных об–следований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку.

При проектировании выборочного наблюдения предполагаются заранее заданная величина допу–стимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения.

В целом формула предельной ошибки выбороч–ной средней позволяет решать следующие задачи:

1) определять величину возможных отклонений пока–зателей генеральной совокупности от показателей выборочной совокупности;

2) определять необходимую численность выборки, обеспечивающую требуемую точность, при кото–рой пределы возможной ошибки не превысят неко–торой, наперед заданной величины;

3) определять вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.

В теории выборочного метода разработаны раз–личные способы отбора и виды выборки, обеспечи–вающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной со–вокупности. Различают два способа отбора: повтор–ный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее об–следования возвращается в генеральную совокуп–ность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара». При таком способе отбора ве–роятность попасть в выборку для каждой единицы ге–неральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, по–сле ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара». Вероятность попасть в вы–борку для каждой единицы генеральной совокупности увеличивается по мере производства отбора.