Джей Форрестер - Основы кибернетики предприятия

DEL — постоянная запаздывания, представляющая среднее время, необходимое для преодоления запаздывания.

Уравнение 8–1 является уравнением темпа и определяет так называемое «неявное» решение [42] См. главу 9. , поскольку оно принимается не по указанию руководителя, а вытекает из существующего в данный момент состояния системы, отображаемого переменным уровнем LEV.

Представление запаздывания неполно до тех пор, пока отсутствует уравнение для определения перемещаемого внутри запаздывания количества LEV. Уровень LEV, находящийся в запаздывании, накапливается благодаря различию в темпах входящего и исходящего потоков:

,

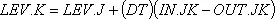где

LEV — уровень, находящийся в запаздывании (единицы);

DT — интервал между последовательными решениями уравнения (время);

IN — темп входящего потока, задаваемый другим уравнением системы (единицы/время);

OUT — темп исходящего потока (единицы/время).

В связи с тем, что запаздывания будут весьма часто употребляться при построении динамических моделей, для их изображения мы будем пользоваться символами (рис. 8–1 б), которые более компактны по сравнению с детализированной диаграммой, приведенной на рис. 8–1 а. На рис. 8–1 б в полуячейке со стороны входа дается обозначение переменной уровня и шифр уравнения, определяющего его величину. В трех ячейках со стороны выхода приводятся символ постоянной запаздывания, номер уравнения, определяющего темп на выходе, и «порядок» запаздывания (DI для первого порядка).

Показательные запаздывания высшего порядка получаются путем проведения потока через два или более последовательно расположенных запаздывания первого порядка. Запаздывания первого и более высокого порядков могут иметь одинаковое общее среднее запаздывание D, но будут различаться по неустановившейся реакции на изменения в темпе потока.

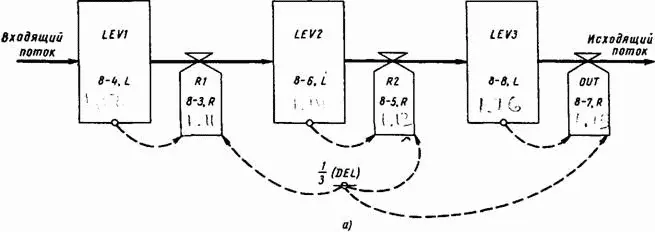
На рис. 8–2 а показано запаздывание третьего порядка в виде общего суммарного запаздывания DEL. Это общее запаздывание распределено на три равные части, каждая из которых представляет собой запаздывание первого порядка. Показательное запаздывание третьего порядка определяется тремя парами уравнений, подобных 8–1, R и 8–2, L, которые связывают между собой темпы потока на входе IN и на выходе OUT:

,

,

,

,

,

,

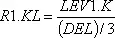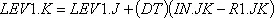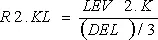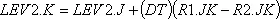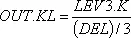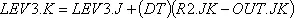Нас в большей степени будет интересовать общее количество LEV, проходящее через данное запаздывание в целом, чем пребывающее в отдельных его секциях. В этом случае можно записать:

.

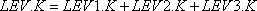Составление уравнений типа 8–3—8-9 и диаграмм, подобных изображенной на рис. 8–2 а, каждый раз, когда нужно представить запаздывание третьего порядка, — весьма трудоемкая операция [43] Уравнения запаздывания третьего порядка могут иметь форму, отличающуюся от формы уравнений с 8–3 по 8–8. . Поэтому мы будем применять в таких случаях сокращенное обозначение. Для нас обычно будет представлять интерес общее перемещающееся в запаздывании количество, описываемое уравнением 8–9; это количество может быть определено непосредственно из уравнения

,

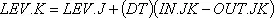которое аналогично уравнению 8–2, L.

Для того чтобы в сжатой форме представить уравнения с 8–3 по 8–8, можно воспользоваться следующим функциональным обозначением:

.

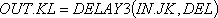Это обозначение не является в собственном смысле слова уравнением; оно лишь указывает на то, что задан необходимый набор уравнений для запаздывания третьего порядка. Здесь « ОUТ » обозначает название исходящего потока; «DELAY3» указывает, что в поток должно быть включено запаздывание третьего порядка, а средняя величина запаздывания равна « DEL ».

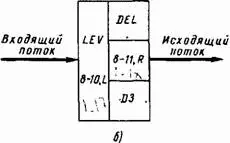
Для обозначения запаздывания третьего порядка достаточно двух уравнений, записанных в форме уравнений 8-10, L и 8-11, R . Если внутренний уровень перемещаемых в запаздывании количеств больше не будет требоваться где-либо в модели, то уравнение 8-10, L может быть опущено. Для обозначения запаздывания третьего порядка будет использован сокращенный символ из рис. 8–2 б, аналогичный приведенному на рис. 8–1 б сокращенному символу для запаздывания первого порядка.

После того как мы рассмотрели математическую форму показательных запаздываний, целесообразно перейти к изучению их поведения. Характерной особенностью неустановившейся реакции запаздывания (то есть изменения темпа исходящего из запаздывания потока во времени) является ее изменение при увеличении числа секций первого порядка в запаздывании.

Рассмотрим прежде всего частный пример запаздывания, связанного с доставкой товаров с завода в оптовую торговую сеть. Неустановившуюся реакцию фактического реального процесса доставки можно лучше всего выявить, если представить себе поставки большого количества товаров на несколько оптовых баз, расположенных в разных местах, выполняемые с помощью различных видов транспорта. В момент, когда в транспортную систему одновременно вводится большое число единиц товаров, на входе в запаздывание, которое отражает эту систему, возникает «импульс»; наша задача заключается в определении темпа поступления товаров в пункты назначения.