Виктор Орехов - Прогнозирование развития человечества с учетом фактора знания

dN/ dT = А·N·(G/N – m)·(1 – k·G/N). (3.1)

Для определения величины G/Nиспользуем приведенное выше выражение (1.11), согласно которому

G = N·(m + γN).

Соответственно уравнение (3.1) может быть преобразовано к виду

dN/ dT = А·γ·(1 – k·m)·N 2· (1 – kγN/(1 – k∙m)). (3.2)

Далее оно может быть представлено в более простом виде

dN/ dT =(1/С)∙N 2 ∙(1 —N/N max ). (3.3)

При N/N max → 0 уравнение (3.3) преобразуется в уравнение типа (1.2), соответствующее гиперболическому росту населения. При N/N max → 1 уравнение (3.3) превращается в уравнение dN/dT = 0, а его решение N =N max . Именно эти два предельных случая использованы для замены неизвестных констант в уравнении (3.2) при переходе к (3.3) с помощью выражений:

А∙γ(1 – k∙m) = 1/С; (3.4)

k∙γ/(1 – k∙m) = 1/N max . (3.5)

При N/N max ~ 1 влияние ограничивающего фактора становится существенным и темп роста численности населения падает. Нормированная функция относительного темпа роста населения

Y = 4(С/N)dN/ dT = 4(N/N max )(1 —N/N max ) (3.6)

представляет собой перевернутую квадратичную параболу (рис. 3.4).

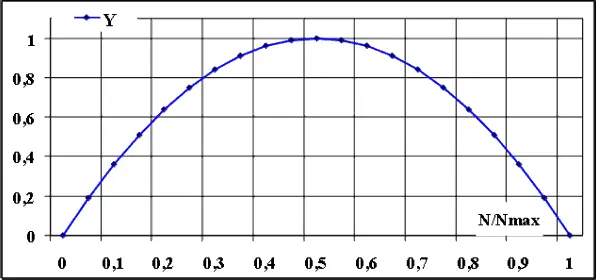
Рис. 3.4. Нормированная функция относительного темпа роста населения

Отметим, что уравнение (3.3) может быть непосредственно проверено на адекватность. Например, при известной производной dN/dT оно позволяет вычислить максимальную численность человечества

N max = N/(1 – C(dN/dT)/N 2 ). (3.7)

Так, в 1995 году скорость роста населения Земли составила dN/dT = 87,4 млн чел. в год, N = 5 682 млн чел. [89]. При С = 160 млрд чел. ∙лет получим, что величина N max = 10 млрд чел., что близко к прогнозируемой максимальной численности человечества, что подтверждает корректность уравнения (3.3).

Решение дифференциального уравнения (3.3) численным методом приведено на рис. 3.5 и обозначено: «F2» (число людей дано в млн чел.). Там же для сравнения дано решение, предложенное С.П. Капицей (F1). Здесь С – константа из уравнений (1.2), (3.3), которая была выбрана из условия наилучшей аппроксимации С = 160 млрд чел. год, а величина N max = 10 150 млн чел.

Из рис. 3.5 видно, что решение данного уравнения относительно незначительно отличается от кривой С. П. Капицы. Наибольшее отличие от статистических данных наблюдается, как и у кривой Капицы, в начале XX века, что является следствием двух мировых войн, пандемии испанки и гражданской войны в России, которые привели к отклонению от теоретической зависимости до 10 %. После 1960 года, т. е. в период демографического перехода, отклонение от статистических данных не превышает 5 %, а от кривой F1 – 3,5 %.

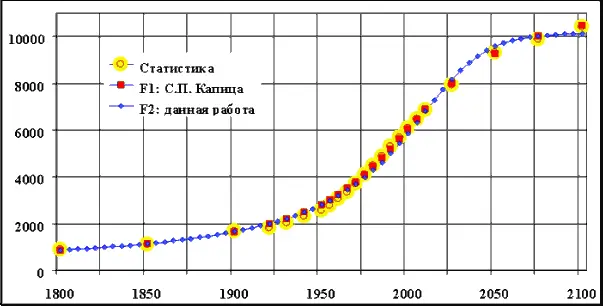
Рис. 3.5. Варианты кривой демографического перехода (млн чел.)

Для более точного сравнения разных уравнений демографического перехода они представлены в табл. 3.1.

Таблица 3.1. Погрешность кривой демографического перехода

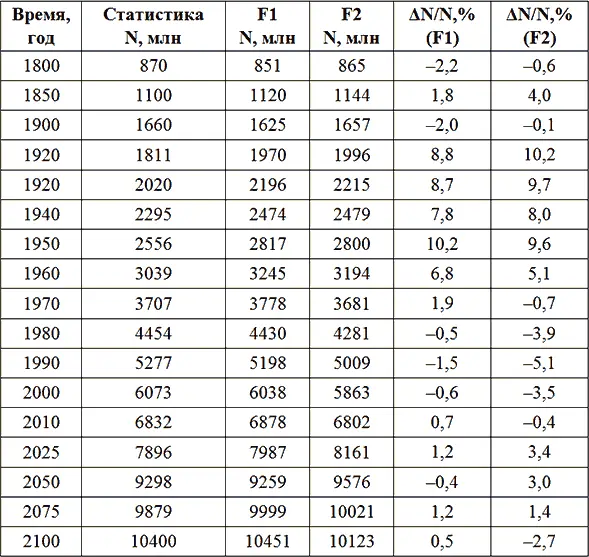
Там же приведены значения численности населения Земли Nпо статистическим данным, на которые опирался С.П. Капица [90]. Здесь ΔN/N– относительное отклонение решения от статистических значений. Видно, что предложенное решение F2 достаточно хорошо согласуется со статистическими данными и еще ближе к теоретической кривой С.П. Капицы, в которой также не могли учитываться такие факторы, как войны и пандемии.

Отметим, что период после 1960 года в мировой истории связан с максимальными темпами экономического роста, отсутствием значительных войн и кризисов, а также быстрым постколониальным развитием стран третьего мира. В этот момент наблюдались быстрые темпы роста населения Земли, которые не только компенсировали потери начала ХХ века, но и привели к превышению реальной численности населения по сравнению с теоретической зависимостью на 3–5 % в период 1975–2000 годов (см. рис. 3.5).

Уравнение (3.3) может быть решено и аналитически. Для этого введем безразмерную переменную Х = N/N max и преобразуем уравнение (3.3) к виду

(1 / (Х 2 (1 – Х))dХ = (N max /С)dT. (3.8)

Решение этого уравнения имеет вид

1/Х – Ln (Х/(1 – X)) = (N max /С)(Т 1 – Т). (3.9)

Возвращаясь к переменной N, получим

T = Т 1 – С/N – (C/N max )Ln(N/(N max – N)). (3.10)

Величина C/N max имеет размерность времени и характеризует время демографического перехода С/N max= N 0T 0/N max≈ 16 лет. Если ввести параметр характерного времени демографического перехода t 1= С/N max= N 0T 0/N max, то мы можем в уравнении (3.8) ввести безразмерный параметр времени t = T/t 1= T × N max/T 0N 0и преобразовать это уравнение в полностью безразмерное, причем в нем не будет ни одного безразмерного параметра подобия. Соответственно решение уравнения в безразмерном виде имеет общий вид

N/N max = F(TN max /T 0 N 0 ) = F(T/ t 1 ).

Характерно, что величина Т 1 при численном решении не является параметром решения и задание начальной точки для расчета, например, N(T=1800 год) или точки, в которой мы хотим получить хорошее согласование результатов, вполне компенсирует отсутствие данного параметра. Дата Т 1 играет роль типа начала координат, и ее изменение приводит к сдвигу всей кривой по времени. Хорошее согласование аналитического решения со статистическими данными достигалось при C/N max =16 лет, N max = 10…10,15 млрд чел. и Т 1 = 2022 год. Аналитическое и численное решения дают одну и ту же зависимость N(T).

Для лучшего понимания смысла полученного решения вернемся к значениям констант Аи kв уравнениях (3.1), (3.2).

Коэффициент k определяет, при каком уровне G/N люди предпочитают наемный труд воспитанию детей (собственно в этом и есть смысл демографического перехода). Размерность k – [чел. × год/долл.]. Из представленного выше выражения (3.5) для константы k видно, что параметр k = 1 /γ∙N max(1 + m/ γ∙N max). Поскольку m/ γ∙N max≈ 0,02, с точностью в 2 % k = 1 /γ∙N max. При N max=10 000 млн чел. 1/k ≈ 10 400 долл./чел.∙год (в междунар. долл. 1995 года).

Коэффициент А характеризует относительную скорость роста численности населения Земли в зависимости от роста ВВП на душу населения, который связан с накоплением знания человечества, в свою очередь зависящего от числа людей. Из выражения (3.4) следует, что величина А = 1/С∙γ∙(1 – k∙m) = 1/С∙γ∙(1 – m/γ∙N max ) ≈1/С∙γ. При С ≈ 16∙10 10чел.∙год коэффициент А ≈ 1/( γ∙С) = 6∙10 -6чел./долл.