Виктор Орехов - Прогнозирование развития человечества с учетом фактора знания

Как отмечал классик теории сложности М. Джаксон, «системная динамика не в состоянии предсказать развитие, если в будущем будут возникать любого рода случайности или качественные изменения среды, например технологические революции или экономические кризисы» [25].

Продолжателем работ по моделированию мировой динамики стал Денис Медоуз [26], который доложил полученные результаты на заседании Римского клуба в 1972 году. Суть этого доклада заключается в том, что при сохранении существующей тенденции к росту человечества уже следующие поколения достигнут пределов демографической и экономической экспансии, что приведет мир к кризису и краху. Для того чтобы избежать глобальной катастрофы, на смену существующей парадигме роста должна прийти парадигма «устойчивого развития».

Детальный анализ исследований, проведенных в данном направлении, дан в работах В.А. Садовничьего, А.А. Акаева, А.В. Коротаева и др. [27]. Там же отмечено, что: «несмотря на большое количество исследований и разнообразных моделей в данной области, в настоящее время моделирование мировой динамики переживает определенный кризис, проявлением которого явилась неспособность внятно предсказать мировые финансово-экономические потрясения 2008 года. Для преодоления существующих проблем необходимо заново осмыслить принципы, положенные в основу моделирования мировой динамики. Надо избежать искуса усложнения моделей, сделать их более прозрачными, при этом не утрачивая, а наращивая уровень их системности».

Тем не менее определенный прогресс в понимании динамики развития человечества был достигнут, причем с использованием относительно простых научных инструментов.

В 1960 году в журнале Science была опубликована работа [28]Х. Форстера, П. Мора и Л. Амиот, в которой показано, что между 1 и 1958 годами н. э. динамика численности населения мира (N) может быть описана при помощи уравнения гиперболы

N ≈ C/(T 1 —T). (1.1)

Здесь Т – время, измеряемое в годах, С ≈ 180 млрд – постоянная с размерностью [чел.∙лет], а T 1≈ 2025 год.

Сергей Петрович Капица [29]обратил внимание на то, что уравнение гиперболы является решением дифференциального уравнения

dN/dT = N 2 / C. (1.2)

Это означает, что темп роста населения Земли в среднем пропорционален квадрату численности населения в данный момент. Скорость роста микроорганизмов при отсутствии дефицита питания описывается уравнением типа dN/dT = N/C, а его решением является экспонента, которая считается одной из наиболее быстро растущих функций. Человечество же росло пропорционально квадрату своей численности. В результате в момент времени T 1≈ 2025 год численность населения, согласно формуле (1.1), должна была бы стать бесконечно большой.

Однако в реальности после 1960 года мир-система перешла в другое состояние, которое называется «демографическим переходом» и характеризуется замедлением темпов роста населения. В дальнейшем, согласно прогнозам [30], численность населения Земли должна выйти на стабильный уровень порядка 9–11 млрд человек, как показано на рис. 1.3.

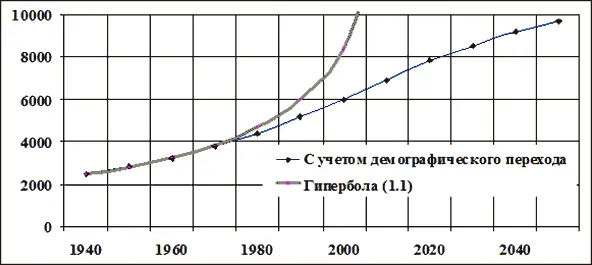
Рис. 1.3. Модели роста населения Земли (млн чел.)

С.П. Капица предложил также уравнение для описания численности человечества на стадии демографического перехода (1.3) и его решение [31](1.4), которое хорошо согласуется со статистическими данными по росту населения Земли:

dN/dT = C/((T 1 – T) 2 – t 2 ); (1.3)

N = (C/t)∙Arcth ((T 1 – T) /t). (1.4)

Однако эти уравнения «не раскрывают сути действующих законов, оставаясь на феноменологическом уровне констатацией обнаруженной эмпирической закономерности» [32].

Важным результатом, полученным С.П. Капицей, является то, что квадратичная зависимость скорости роста от численности человечества на гиперболической стадии свидетельствует о наличии коллективного взаимодействия. Оно «…определяется механизмом распространения и размножения обобщенной информации в масштабе человечества» [33]. Однако более детального представления о том, что такое «обобщенная информация», как она распространяется, как влияет на рост человечества и почему столь резко снижается ее влияние в период демографического перехода, в работах С.П. Капицы нет.

Существенный вклад в понимание данного вопроса сделал А.В. Подлазов, который обосновал, что свойство единства человечества как системы с самого начала ее существования могло обеспечивать только распространение «жизнесберегающих технологий» [34]. Уровень развития этих технологий Рон определил [35]через уменьшение среднего коэффициента смертности k d , которое достигается благодаря их действию, т. е. Р = k d – k d0 , где k d0 ≈ 0,06 год –1– коэффициент смертности первобытного человека. Предполагается, что все человечество характеризуется единым уровнем этих технологий. До демографического перехода средний коэффициент рождаемости k b можно считать приблизительно постоянным и равным k b0 ≈ k d0 . Таким образом, скорость роста народонаселения определяется формулой

dN/dT = PN. (1.5)

Для определения зависимости уровня технологий от времени А. В. Подлазов предлагает формулу, которая имеет вид

dP/dT = PN/C, (1.6)

где константа С определяет трудозатраты, необходимые для увеличения Р в е раз при постоянном N.

Интегрируя систему (1.5) – (1.6), А.В. Подлазов получает уравнение, которое он называет «основным уравнением теоретической демографии» [36]

N = CP. (1.7)

Подставляя его в (1.5), получим уравнение для роста человечества (1.2).

В этих построениях есть довольно спорные допущения. Так, согласно формуле (1.6), с ростом уровня технологий производительность труда каждого изобретателя пропорционально возрастает, что вовсе не очевидно. Здесь следует напомнить о работе Дж. А. Хюбнера, в которой утверждается, что количество крупных технических изобретений за год, деленное на численность населения мира после 1915 года, падает (рис. 1.4) [37].

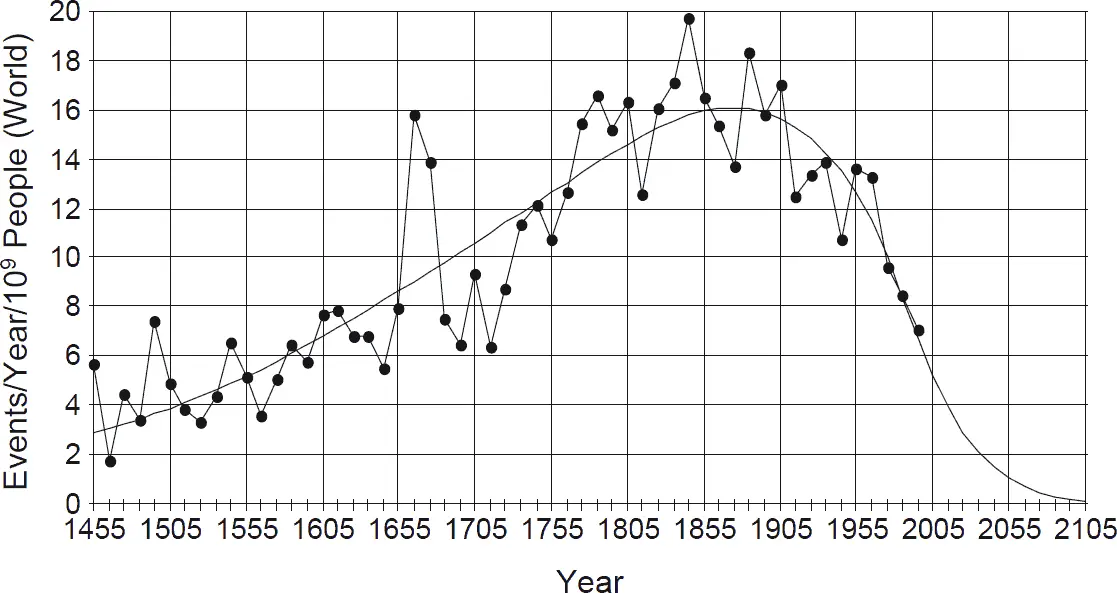
Рис. 1.4. Число крупных изобретений в год на миллиард жителей мира

Аналогичный подход к определению уравнения для темпов роста технологий использует и М. Кремер [38], хотя он определяет уровень технологий через уравнение для мирового ВВП (G)