Владислав Масликов - Универсум. Общая теория управления

…новое положение должно находиться в согласии не только с хорошо зарекомендовавшими себя теориями, но и с определенными общими принципами, сложившимися в практике научных исследований. Эти принципы разнородны, они обладают разной степенью общности и конкретности, соответствие им желательно, но не обязательно. Наиболее известный из них – принцип простоты, требующий использовать при объяснении изучаемых явлений как можно меньше независимых допущений, причем последние должны быть возможно более простыми… принцип привычности (консерватизма). Он рекомендует избегать неоправданных новаций и стараться, насколько это возможно, объяснять новые явления с помощью уже известных законов… Принцип универсальности предполагает проверку выдвинутого положения на приложимость его к более широкому классу явлений, чем тот, на основе которого оно было первоначально сформулировано… Согласно принципу красоты, хорошая теория должна производить особое эстетическое впечатление, отличаться элегантностью, ясностью, стройностью и даже романтизмом… Помимо указанных, имеются многие другие общие принципы, используемые при оценке новых идей и теорий [31, 312].

Во-первых, несомненно, необходимо определение минимального, базового количества философских категорий. Сколько их должно быть? Три? Одна? Семь? Восемь? Поскольку в основе любого процесса познания лежит дуальная природа, то исторически и логически обоснованный ответ на распознающий любые ОЯП окружающего мира диалектический вопрос различения «это или не это?» может быть только таким: количество базовых предельно обобщённых философских категорий должно быть равно двум. Именно из дуальности должны выводиться все остальные философские категории практически состоятельного описания.

«Дополнительности принцип – методологический принцип, выдвинутый Бором в связи с интерпретацией квантовой механики. Его можно сформулировать так: для воспроизведения целостности явления необходимо применять в познании взаимоисключающие «дополнительные» классы понятий» [68. 138].

Этот древний принцип [1], сформулированный Бором применительно к современной ему квантовой механике, можно толковать гораздо шире. Из этих категорий вытекают два связывающих диалектически взаимоисключающие дополнения варианта взаимодействия между ними, выраженные в формулах логики как

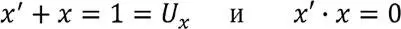
(1.1)

В параллельности, единичности существования взаимно дополняющих друг друга x и x’ отражён Универсум [2], – это эквивалент понятий «Всё как целостность» или «полный Универсум», в последовательности как взаимоисключении – логическом произведении x на его дополнение x’ – антипод «Ничто» или «пустой Универсум» [3]. Следует подчеркнуть, что дуальное и неразрывное представление объектов Мироздания вполне допустимо. Как в двоичной арифметике понятие «1» неотделимо от противопоставляемого ему понятия «0», причём оба эти состояния в совокупности дают понятие «числовой разряд», точно также любой объект Мироздания можно представить как Универсум. Он необходимо включает в себя два и противоположных и одновременно взаимосвязанных значения, которые в логическом описании обозначаются инверсными переменными x’ и x. Это означает, что если x’=0, то x=1 и наоборот, если x’=1, то x=0. Формулы, представляющие взаимосвязь дуальности (1.1) выражают не что иное, как дискретную возможность существования (логическая единица) или несуществования (логический ноль) Универсума, которым можно представить любой ОЯП Мироздания.

Универсум (U) – это та самая единица, природу и смысл появления которой в различных уравнениях не могут пояснить ни школьные учителя, ни преподаватели высшей школы. Универсум связывает две дополняющих друг друга противоположности в единую диалектическую целостность, составляющую базовую основу всех логических и вытекающих из них математических формул. Это базовое дискретное описание ОЯП, которое может быть представлено любым количеством составляющих компонент – логических переменных.

Так, для системы их двух логических переменных U x=x’+х и U y=y’+y формулы, описывающие дискретный универсум, могут выглядеть следующим образом:

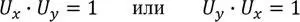
(1.2)

Конъюнкция (1.2) двух исходных универсумов – логических переменных U x и U y представляет качественно новый универсум, образованный совпадающими элементами множеств U x и U y . Логическая единица – это универсальный функтор существования, граница между преимущественно качественным логическим и преимущественно количественным математическим описанием ОЯП внешнего мира. В аналоговом, математическом приложении это означает то, что существующий универсум системы, состоящей из двух выраженных числами множеств – категорий a и b также должен быть равен единице, т. е.

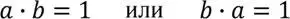
(1.3)

Это – базовое аналоговое описание Универсума. С дискретным его связывает то, что в обоих описаниях Универсум может существовать только в том случае, если любая переменная, входящая в его состав, не представляет собой Ничто (пустой Универсум).

Для цифровой величины x’ это означает, что для любой логической величины непременно существует её дуальный антипод x , т. е. логически подтверждается дуальность Мироздания. Для аналоговых величин a и b (1.3) это, соответственно, значит то, что предел уменьшения/увеличения [4]одной величины непременно соответствует обратному процессу – увеличению/уменьшению второй величины, что описывается также известными соотношениями

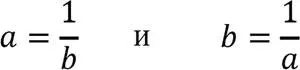
(1.4)

Ввиду того, что статистически значимые объёмы аналоговых математических ( а, b ) понятий в реальном мире существенно больше объёмов дискретных логических ( x’, x ) [5], для полного описания реальных систем необходимы ещё две категория – категории взаимного соотношения дуальных величин. Она открывает возможность сравнения а с b и наоборот, т. е. установления относительной, взаимообратимой Меры ( Z ) одной величины относительно другой

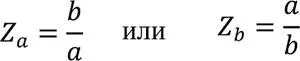
(1.5)

Таким образом, дихотомия Мироздания трансформируется в квадролектическую систему, в которой Универсум как целостность представлен четырьмя категориями: двумя взаимодополняющими друг друга величинами а и b , а также взаимообратимыми соотношениями Z а и Z b . Свойство обратимости позволяет вместо двух качественно эквивалентных вариантов мерных соотношений Z обойтись одним из них [6], например, Z а . Учёт обратимости означает, что целостная система ОФК может быть триалектической, содержащей две взаимодополняющие категории а и b и мерное отношение между ними Z . Введение какой-то новой категории уже не будет соответствовать соблюдению известного принципа простоты.