Александр Бакулин - Гравитация и эфир

Проиллюстрируем наши предположения простейшим примером, не претендующим сейчас на большую степень приближения к истине, однако вполне объясняющим чёткую физику «видимых» сгущений звёзд в потоках четырёх рукавов. Сразу скажем, что, например, физика постепенного уширения шагов спиралей при удалении рукавов от центра Галактики весьма сложна и зависит сразу от многих факторов, которые мы, естественно, предполагаем, но здесь просто не обсуждаем. Но сосредоточимся на неких средних шагах неких гребней волн гравитации, которые могут совпадать, допустим, именно с теми концентрическими окружностями, обозначенными штриховыми линиями и следующими через шаг в 2 кпк. Пусть, для начала некоторых наших почти «от фонарных» предположений, две гигантские массы отстоят друг от друга также на 2 кпк и вращаются по самой малой окружности, а «сейчас» находятся в точках 1 и 2.

Сейчас мы попробуем показать некоторую гравитационную чувствительность всей системы Галактики, то есть вычислим порядок возможных амплитуд гравитационных волн. Для этого из закона всемирного тяготения найдём порядок силы F, действующей, например, на пробное тело (помещённое в точку 11) для двух взаимных расположений масс: 1–2 и 4–6. Все расстояния примем за относительные, где один килопарсек (1 кпк) примем за «единицу» (1). Для «базы» – радиуса точки 11 (0–11), равной 11-ти единицам, и измеренному графически углу 1–11–2 ( 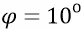), найдём радиус 1–11 (2–11). В прямоугольном треугольнике 0–1–11 угол между катетом 0–11 и гипотенузой 1–11 составляет .

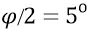Тогда:

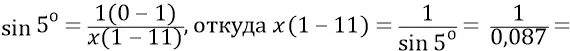
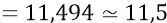
Пусть теперь масса тела точки 11 будет равна каждой из масс m тел точек 1 и 2 и равна 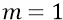. Имеем на это полное право, когда решаем чисто кинематическую задачку о порядке разности в силах гравитации между центральным телом (система 1–2) и пробным (11). Тогда для положения колеблющихся тел 1–2 будем иметь:

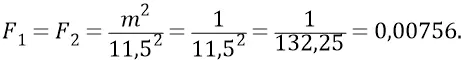
Суммарная сила, действующая на тело 11 от тел 1 и 2;

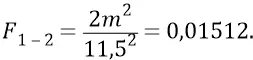
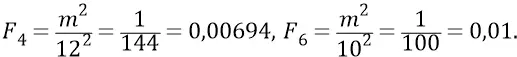
Сумма сил 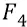и 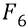в положении 4–6 вращающихся масс:

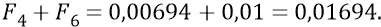
Сразу же замечаем, что гравитационная сила, действующая на тело 11 со стороны «разноудалённых» колеблющихся масс положения 4–6, больше, чем сила от этих же масс в их положении «равноудалённых» 1–2:

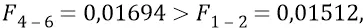
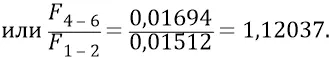
То есть сила гравитации даже для наиболее удалённых звёзд рукавов Галактики колеблется, для двух ортогональных положений масс центральной «двойной звезды» на 12 % величины этой силы. Это очень великая разница в периодических колебаниях силы гравитации, не заметить которую было бы просто невозможно. Поэтому Природа очень хорошо «замечает» эту силу, рисуя нам свою ощутимую подсказку, на которую, однако, наши физики обращают пока слабое внимание, если вообще как-то мыслят в этом направлении.

Здесь надо сразу же заметить, что, естественно, эта сила будет иметь меньшую амплитуду, причём, значительно меньшую, если база между телами 1–2 (4–6) будет значительно сокращаться. Однако поскольку физики не видят область нашей самой малой окружности (она полностью скрыта «центральной пылью» Галактики), но начинают видеть только рукава, отходящие от центра даже не на 1 кпк (радиус нашей малой окружности), но на 3 кпк (радиус начал рукавов), то мы имеем полное право предположить то, что уже предположили: наши колеблющиеся массы находятся «глубоко в пыли», то есть в той области, которая очень плохо различима астрофизиками.

И поскольку картинка Галактики явно динамическая, то теперь мы перейдём от статической её геометрии к некоторой предполагаемой динамике колебаний центральных масс, то есть перейдём к динамике распространения радиальных гравитационных волн. Сначала выразим шаг спиралей Галактики (грубо принимаем его за величину 2 кпк) не только в световых годах, а также не только в «световых днях», но в «световых часах» – как в тех расстояниях шага спиралей, которые свет пробегает за 1 час:

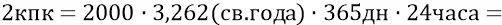
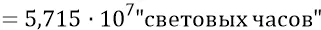
Но, имея в виду, что гравитация быстрее света в 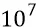раз (в самом грубом приближении), найдём, что гравитационная волна от колебаний наших масс будет преодолевать шаг спирали Галактики в 2 килопарсека за время:

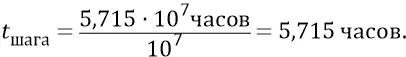
Всего-то. За это время ни одна из звёзд любых рукавов не сдвинется на «заметное» нам в масштабах картинки расстояние, то есть все звёзды Галактики будут стоять на своих местах «как вкопанные». Но при этом в любых угловых радиальных направлениях могут пробегать гравитационные волны, с их какими-нибудь «гребнями», следующими через каждые 5,715 часов, для каждой из точек (звёзд) рукавов.

Однако сразу же замечаем, что условия нашей кинематической задачки к реальности не могут иметь никакого пока отношения, поскольку для полученного нами желаемого времени пробегания гравитацией каждого отрезка в 2 кпк за 5 часов, массы центральных «звёзд» при базе между ними в 2 кпк должны были бы двигаться с линейными скоростями, на много порядков превышающими скорость света. Прикинем порядок этих скоростей. Линейные скорости центральных «масс» Галактики:

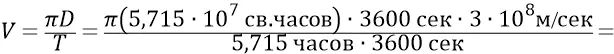
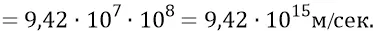
Для того чтобы вписаться в более-менее реальную физику, уменьшим линейные скорости наших масс до величин, допустим, одной десятой от скорости света (хотя, и эту величину надо было бы, «для порядка», слегка уменьшить ещё хотя бы в несколько раз; но оставим так). Для этого придётся уменьшить базу между массами в 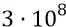раз. Тогда получим: