Александр Бакулин - Гравитация и эфир

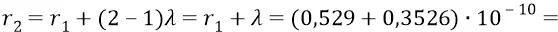
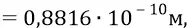
и так далее – для следующих орбит.

Затем вычисляем значения напряжённостей поля на уровнях орбит по нашей формуле (повторим её здесь для первой орбиты:

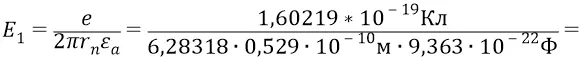
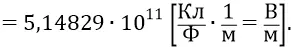
В следующем столбце таблицы вычислены потенциальные энергии атомной системы для уровней орбит по классической формуле:

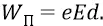
Здесь e – это заряд электрона, перемещаемый в поле протона (Е); вообще говоря – из бесконечности (как из точки нулевого потенциала поля протона) в точку нахождения электрона (на какую-то атомную орбиту). Но уточним – чем является здесь расстояние d для нашего случая «атомного конденсатора». Вспомним, что потенциальную энергию атомной системы в основном состоянии атома (для уровня первой электронной орбиты) мы уже находили, отталкиваясь от практического значения энергии ионизации 13,6 эВ. Для сдвинутой «вниз» энергетической шкалы с нулевым уровнем энергии, соответствующим удалению электрона на бесконечность, то есть уровню свободного от атома электрона, уровень потенциальной энергии атома оказывался вдвое меньшим полной энергии атома (–13,6 эВ) и составлял величину

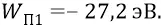
При этом тем потенциалом, под которым находился электрон первой орбиты, был потенциал (–27,2 В). Проверяем:

если потенциал поля первой орбиты равен (–27,2 В), то потенциальная энергия атомной системы с электроном в ней на первой орбите равна –

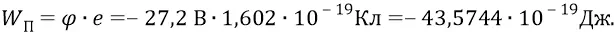
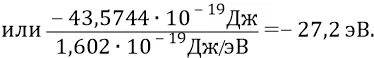
Но тогда то расстояние d , на которое был перемещён заряд электрона для того, чтобы поместить его в потенциал (–27,2 В), определится следующим образом:

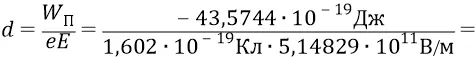
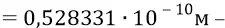
это радиус удаления первой орбиты от протона – как источника поля «атомного конденсатора». То есть если одна «обкладка конденсатора» у нас заряжена положительно (протон – источник поля), то вторая обкладка заряжается отрицательно (отрицательный электрон с зарядом 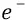и уровнем напряжённости орбиты – E, отнесённой от источника поля на расстояние d ).

Однако далее мы вправе выбрать уровень напряжённости поля первой орбиты 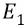за тот начальный, от которого затем, по мере удаления от ядра на уровни следующих орбит, напряжённость поля будет убывать в соответствии с множителем удаления – 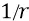(функция гиперболы).

Здесь сделаем важное замечание. Классический пример конденсатора – это конденсатор с параллельными друг другу обкладками равной площади. Существенно то, что поле E внутри такого конденсатора – однородное. И поэтому в нём электрическое поле E при перемещении заряда (у нас – электрона) совершает работу:

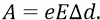
Причём эта работа электростатической силы в консервативной потенциальной системе, во-первых, не зависит от формы траектории перемещаемого заряда, во-вторых (по определению) равна изменению потенциальной энергии, взятому с противоположным знаком:

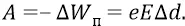
В нашем же «атомном конденсаторе» поле Е – неоднородно и изменяется по закону Следовательно, выбирая за точку отсчёта поля его уровень на первой орбите 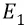, мы можем записать:

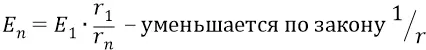
с ростом номера орбиты n .

Но потенциальная энергия системы 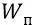в поле источника изменяется в зависимости от 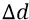– как от расстояния точки нулевого потенциала (бесконечность) до точки «около источника поля», при том, что поле E в формуле для потенциальной энергии 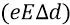однородно, то есть неизменно вдоль каждой силовой линии. То есть для того чтобы воспользоваться формулой, связывающей потенциальную энергию 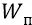, поле E и расстояние d , нам надо как бы выровнять наше неоднородное поле и сделать его как бы (по исходной формуле для потенциальной энергии плоского конденсатора) однородным, то есть таким, когда заряд, удаляясь от источника поля (от положительной обкладки конденсатора), двигался бы по одной и той же неизменной силовой линии поля, не убывающей по закону 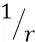, но остающейся неизменной по силе её воздействия на заряд (электрон).

Но сейчас мы сделаем хитрый ход (по отношению к задаче получения требуемой формулы, согласующейся и с теорией о потенциальной энергии, и с реалиями изменения поля в «атомном конденсаторе». Мы перенесём закон 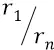от изменения по нему напряжённости Е на изменение по нему перемещения заряда 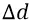в поле источника. При этом учтём тот факт, что в нашем «конденсаторе» перемещение заряда по удаляющимся орбитам происходит равномерными дискретами

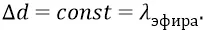
Запишем формулу:

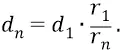
В ней закон изменения расстояния орбиты от её номера n – квадратичный и точно такой же 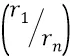как закон изменения напряжённости 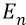в зависимости от номера орбиты n . Так, при очень больших номерах n расстояние 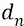стремится к нулю, то есть стремится к точке нулевого (самого «высокого» по номерам орбит) потенциала поля источника. По мере же уменьшения номера орбиты величина 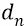растёт, достигая самого своего большого значения 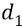в точке орбиты 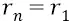. 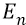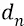Поэтому, сравнивая формулы для и в зависимости от члена 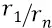(закон 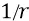), мы можем воспринимать закон изменения потенциальной энергии не в зависимости от изменения перемещения заряда в однородном поле, но в такой же зависимости изменения напряжённости поля (теперь – неоднородного) в равномерном «пересчёте» номеров орбит: