Александр Бакулин - Гравитация и эфир

Однако мы сильно отвлеклись от конкретики обсуждаемой темы атомных орбит. Но сначала – снова классика. Напомним школьнику, что такое потенциали напряжённостьполя. Квантовая физика сильна тем, что она может (наконец-то!) объяснить школьнику физический смысл тех макро-характеристик электростатики и электродинамики (типа «потенциала», «напряжения», «напряжённости»), о которых школьник уже слышал, но очень плохо их понимает (мы это утверждаем, то есть утверждаем то, что школьник плохо понимает все эти характеристики).

Итак, во-первых, затронем некоторые основы электростатики. Что такое «заряд» вообще и заряд электрона – в частности? Для электростатики «заряд» – это просто электрическое поле частицы – как поток квантов, «излучаемых», например, электроном («из электрона») во все от него стороны пространства. Электрон – это стандартная космическая частица, которая всегдапребывает в стандартном космическом эфире, имеющем стандартные космические характеристики (такие как плотность распределения квантов – частиц, скорость их движения, масса этих частиц, их конструкция и наконец – их «полярность» – как некоторое чисто конструктивное отличие друг от друга «положительных» квантов – частиц эфира от «отрицательных» частиц этого же эфира, о чём физики пока ещё абсолютно не знают). Кстати, физики не только не знают, что такое «электрический заряд», но они не знают, что такое электрон.

Во-вторых, сейчас (объясняя «заряд») мы находимся внутри атома, где действуют (взаимодействуют) два «заряда»: «заряд электрона» и «заряд протона». Заряд электрона, с точки зрения объяснения характеристик электростатики, мы жаргонно будем называть словом «электрон» и обозначать его символом « 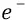» (то же делают и физики, и это « 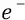» стоит и у физиков, и у нас в формулах). То есть мы в контексте данных (электростатических) объяснений не говорим об электроне, как о частице, имеющей массу, конструкцию, скорость, собственную частоту вращения, но говорим лишь о поле этой частицы, как говорим и о поле частицы – протона.

В-третьих, и заряд электрона (как поток – поле всегда излучаемых им частиц эфира), и заряд протона (как аналогичный поток излучаемых им частиц) в атоме (для простоты – одноэлектронном, то есть в атоме водорода), эти потоки – жёстко поляризованы, как и жёстко поляризованы сами частицы – электрон и протон. То есть вся картинка их взаимных полей лежит строго в одной и той же «тонкой-тонкой» плоскости, в пределе имеющей «толщину» размера частицы – электрона, совпадающую с «толщиной» частиц-кварков, из которых состоит протон, которые (эти там кварки) быстро вращаются внутри протона, являя нам некоторое «колёсико», излучающее из себя во все стороны этого «колёсика» суммарное поле протона (но излучающее строго – в плоскости этого колёсика), поле, состоящее, вообще говоря, из суммы полей кварков, но в результате равное по величине (по силе) точно такому же «заряду», который излучает электрон.

И теперь, словно бы «конструируя» атом, мы будем плавно вносить откуда-то очень издалека (в пределе – из бесконечности) отрицательный «электрический заряд» (частицу электрон вместе с его полем) в потенциальном полеположительного «электрического заряда» (протона-частицы, вместе с его полем). То есть мы будем совершать работупо перемещению единичного заряда (электрона) в потенциальном поле – из бесконечности в какую-то точку внутри атома, на уровень удаления какой-то орбиты от протона. Поскольку в данной главе мы занимаемся лишь некоторыми оценочнымицифрами (точными займутся физики, если захотят, а не захотят – займутся школьники), то для простоты будем вносить электрон на уровень, допустим, n – ной орбиты атома. Почему именно n – ной? Если мы внесём электрон на уровень первой орбиты, то он окажется под потенциаломполя протона уровня десятка вольт, а если внесём его на уровень n – ной орбиты, то он окажется там под потенциалом поля протона величиной всего лишь, допустим, в десятые доли вольта (эти потенциалы вычисляются физиками в общем случае методами спектроскопии). То есть разность потенциалов поля протона в точках первой и n – ной орбит составит величину напряжениямежду этими точками:

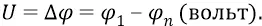
Самым важным результатом здесь будем считать тот, что разность потенциалов (напряжение) между точкой первой орбиты и точкой n – ной орбиты почтиравна разности потенциалов (напряжению) между любой из точек первой орбиты и «бесконечностью».

Зачем нам понадобилось привязывать потенциалы к орбитам 1 и n? Это нужно только для того, чтобы задать точное расстояние между двумя фиксированными точками потенциального поля протона – ∆d. Потому что расстояние между любой точкой поля вблизи протона и далёкой бесконечностью (как истинное ∆d для истинного потенциала) измерять, мягко говоря, неудобно. Но это ∆d нам необходимо знать потому, что классика физики определяет через него напряжённостьполя (поля протона, в данном случае):

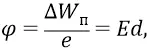
где 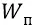– потенциальная энергия нашего «пробного» заряда (электрона – как «заряда»), внесённого из бесконечности в данную точку потенциального поля протона;

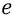– заряд электрона, как поле этого заряда (о нём мы поговорим ещё более подробно – ниже);

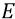– напряжённость электрического поля протона в точке внесения «пробного заряда» (электрона);

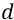– расстояние между точкой нулевого потенциала и данной точкой потенциального поля протона; здесь важно то, что (в нашем примере с n – ной орбитой) расстояние между n – ной орбитой и бесконечностью равно не бесконечности, но мы его принимаем «нулевым», так как ведём отсчёт потенциала не от бесконечности, а, в первом приближении, от n – ной орбиты, где потенциал (между n – ной орбитой и бесконечностью) мало отличается от «нуля» (от потенциала бесконечно удалённой точки – как потенциала истинного там «нуля»).

Начнём с закона, проверенного временем. Таким, главным в электростатике, является закон Кулона:

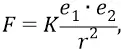
где заряды 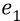и 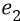мы обозначаем символами, принятыми в теории Бора и квантовой механике;