Александр Бакулин - Гравитация и эфир

Протон тоже является космическим резонансом. Там тоже всегда резонируют три электромагнитных тела: каждые два противоположных кварка в конструкции протона и всё тот же эфир. Правда, там работает другой слой эфира-вакуума, более высокочастотный. Этот «высокочастотный» эфир собран гравитацией в область космоса, которая называется Метагалактикой.

Электрон – это тоже космический резонанс. Там, в нём, резонируют тоже три тела: ядро электрона, сделанное из преонов, орбитальные преоны, создающие каждое электромагнитное кольцо электрона, и преонныйвакуум, работающий там в виде поля ядра электрона. И этого работающего там преонного тела в природе космоса – ещё более «видимо-невидимо», чем видимо-невидимо электромагнитного эфира во Вселенной.

Сама Вселенная – это тоже космический резонанс. Там рабочим телом является гравитация, в лице квантов-частиц гравитационного вакуума. Гравитация во Вселенной удерживает в её пульсирующем объёме весь электромагнетизм, который зародился там в начале самой первой пульсации Вселенной.

Везде в космосе, где есть какая-то оформленная Им Система, нужно поискать соответствующий резонанс, который там обязательно должен быть.

Теперь рассмотрим два конкретных примера в механике атома, которые продолжаютклассический путь исследования атомных процессов. Физики – квантовомеханики таких примеров не только не рассматривают, но не хотят, причём категорически не хотят рассматривать. И даже только этим своим нежеланием они фактически обманываютшкольника, не позволяя ему, следовательно, разобраться с физикой атома. А не разобравшись с физикой, бесполезно потом городить многоэтажную математику теории «квантовой механики».

В первом примере (рис. 21.5) мы рассмотрим кинематику перехода электрона с первой орбиты (базовой – стационарной) на вторую (возбуждённую). Причём надо понимать, что вторая орбита является «возбуждённой» лишь по отношению к той первой «невозбуждённой», которая является таковой для данной, относительно низкой температуры. Но при какой-то повышенной температуре основной орбитой может быть не первая, но как раз вторая, которая при этой более высокой температуре превратится в «базовую-стационарную».

Похоже на то, что для всех самостоятельно светящихся тел базовой стационарной орбитой является не первая «боровская», но вторая «бальмеровская», с которой, поскольку она всё же «возбуждённая» какими-то процессами, электрон постоянно норовит перескочить-опуститься на первую, излучая при этом фотон видимой нашим глазом частоты (из серии Бальмера таких фотонов). Это не значит, что при этой температуре будут отсутствовать кванты (фотоны) серии Лаймана – как серии перехода электрона с возбуждённых орбит на первую боровскую, но таких переходов при такой температуре просто будет меньше в подавляющем большинстве там бальмеровских, когда возбуждённые электроны возвращаются с высоких уровней на вторую бальмеровскую орбиту.

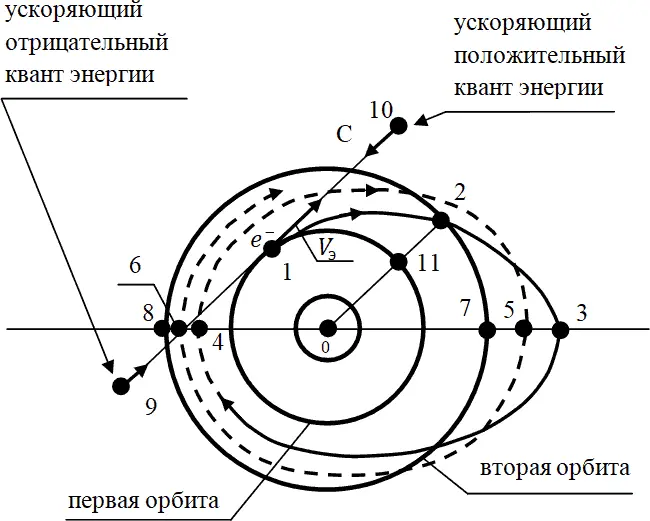
Рис. 21.5.1

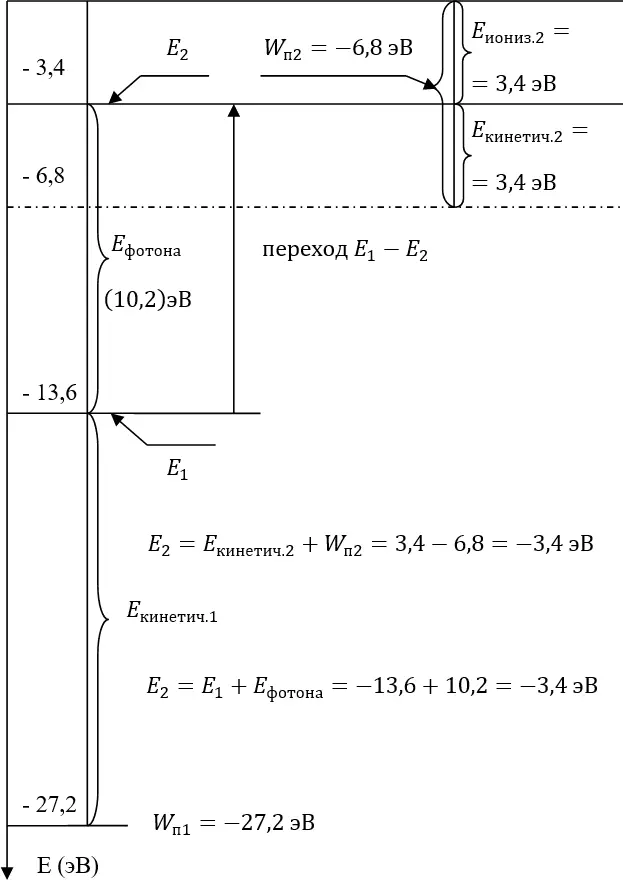
Рис. 21.5.2

Полная энергия атома для уровня второй орбиты, по расчётам квантовомехаников, составляет величину «минус 3,4 эВ», хотя у нас к этой цифре могут быть вопросы. Это значит, что энергия «минус 3,4 эВ» является тем математическим ожиданиемдля уровня энергии, который характерен для второй стационарной атомной орбиты. Но поскольку при такой данной температуре атом постоянно «дышит», возбуждаемый внешними «тёплыми» и видимыми фотонами, включая и редкие ультрафиолетовые и ещё более редкие в отношении каких-то наших «нормальных» условий – рентгеновские фотоны (очень энергичные), то полная энергия атома постоянно колеблется то вверх, то вниз, но колеблется около её «математического ожидания» – «минус 3,4 эВ». На нижней диаграмме рисунка 21.5 она колеблется от средней 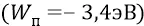в пределах от «0» до .

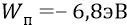При этом мы отлично видим, что уровень этих плюс-минус колебаний в среднем равен уровню кинетической энергии электрона, которой этот электрон обладает на второй орбите.

Такие отклонения от среднего в плюс-минус сторону в математике называются « дисперсией». То есть для второй (бальмеровской) орбиты мы имеем:

математическое ожидание –

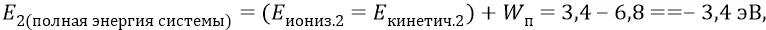
дисперсия –

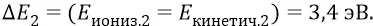
При этом дисперсия имеет знак отклонения от математического ожидания (от среднего) в обе стороны, приводя к колебаниям полной энергии в пределах от

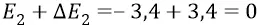
до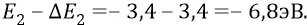

Исследуя таким образом любую атомную систему, мы приходим к удивительно простому по своей физике результату:

математическим ожиданием значения энергии системы, как её средним значением, является полная энергия атома –

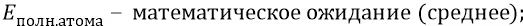
дисперсией системы является кинетическая энергия орбитального движения электрона.

Действительно, если мы остановим движение «заряда» – электрона на уровне его орбиты, обнулив таким образом его кинетическую энергию, то у системы останется лишь потенциальная энергия с «зависшим» в поле протона зарядом Но какой будет эта потенциальная энергия?

Ещё раз. Когда электрон вращался на уровне второй орбиты – как в стационарном состоянии атома, то у него была какая-то полная энергия (а на самом деле – не «у него», а у атома) – как средняя энергия этого состояния атома. Но если мы из этой средней энергии убираем (всегда положительную) кинетическую энергию движения электрона по этой орбите, то значение оставшейся энергии атома должно «провалиться» (отклониться от среднего в «минус» сторону) на значение кинетической энергии. Значит истинной потенциальной энергией атома с «зависшим» неподвижным электроном (при этом остаётся «голая» электростатика без электродинамики) является следующая: