Владимир Левшин - Магистр Рассеянных Наук

— А Магистр ей вовремя помешал, не то не сносить бы ей головы! — сказал Нулик.

— Единичка делила совершенно правильно, за что ж её казнить? — возразила Таня. — Если через точки деления радиуса провести из центра круга четыре концентрические окружности, то круг разделится на пять частей, относящихся друг к другу, как 1:3:5:7:9.

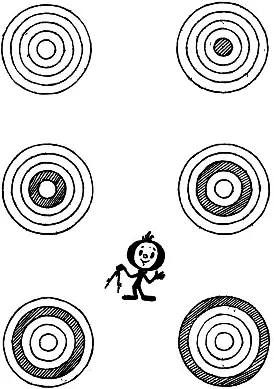
— А как ты это докажешь? — спросил Нулик, оседлав своего любимого конька.

— Сейчас увидишь. Примем радиус внутреннего маленького круга за единицу и вычислим его площадь по формуле π·r 2. Что мы увидим? Мы увидим, что площадь этого круга равна π: ведь единица, возведённая в квадрат, так и останется единицей, а коэффициент единица, как мы знаем, не пишется.

— Убедительно! Но как ты вычислишь площадь кольца, следующего за внутренним кругом?

— Очень просто. Единичка разделила радиус большого круга на пять равных частей. Значит, если радиус малого круга принят нами за единицу, то расстояния между всеми соседними концентрическими окружностями тоже равны единице. И для того чтобы вычислить площадь соседнего с малым кругом кольца, надо вычислить разность площадей двух кругов: одного с радиусом, равным двум, и другого — с радиусом, равным единице. По той же формуле π· r 2площадь круга с радиусом два равна 4π. Вычитаем из 4π площадь малого круга — π и получаем 3π.

— Все равно что вычесть из бублика его дырку, — снова сострил Нулик.

Его неожиданное и точное сравнение насмешило всех, даже строгую Таню.

— Нагляднее не придумаешь! — сказала она. — И потому остальное решай сам.

— С удовольствием! Из площади круга с радиусом, равным трём, вычтем площадь круга с радиусом, равным двум. Получим 9π-4π=5π. Теперь тем же макаром найдём площадь предпоследнего кольца: 16π-9π=7π а там — и последнего: 25π−16π=9π. Что и требовалось обнаружить! Площади пяти частей круга равны: π, 3π, 7π и 9π.

— И, значит, относятся они, как 1:3:5:7:9, — подытожила Таня. — Так что казнить Единичку не за что!

— Но ведь её могли казнить ни за что, ни про что! — возразил президент. — Этот антипод Альбертини-Джерамини такой негодяй!

— Что негодяй — не спорю, — согласился Олег. — Но только не антипод.

— Думаешь, антипод для него слишком сильно сказано? — спросил Нулик.

— С чего ты взял, что антипод — слово оскорбительное? Антиподами называют людей, живущих на противоположных точках земного шара. Вот, например, жители Европы и жители Америки — самые настоящие антиподы.

— Антипод, антипод… — со смешком повторил про себя Нулик. — Чудное слово.

— Ничуть! — сказал я. — Обычное греческое слово, состоящее из двух частей: анти значит «против», а подос — «нога».

— Ой, не могу! — закатился Нулик. — Выходит, американцы ходят кверху ногами?!

— С точки зрения географической и по отношению к европейцам — да. Ведь земля — шар! Но вообще-то слово «антипод» больше употребляется в смысле переносном. Так называют людей, с противоположными взглядами и характерами. Так что по отношению к Альбертини и Джерамини слово «антипод» никак не применимо — ни в прямом, ни в переносном смысле: ведь это один и тот же человек!

— Время, время! — сказала Таня, озабоченно взглянув на часы. — Уж очень мы распространяемся. Переходим к задаче мини-Джерамини.

— Какая же это задача? — возразил Нулик. — Сразу видно, что Магистр просто пошутил или забыл правила деления. Разделить 48 на 8 и получить 51!

— Да, — согласился Сева, — это уж не математика, а цирковой трюк. Давайте лучше выясним, сколько времени отдыхал Мини на взморье.

— Вы как хотите, а я этой задачи не раскусил! — сознался Нулик.

— Ни раскусывать, ни закусывать здесь нечего, — сказал Сева. — Разве что запивать. Такие задачи только и решать, что за чашкой кофе.

— Кейфуя? — щегольнул президент новым для него словечком.

— Думаешь, кейфовать — это от слова кофе? — спросил я.

— Разве нет? — растерялся Нулик.

— Ничуть не бывало. «Кейф» — по-арабски «послеобеденный отдых».

— Хоть тут Магистр не ошибся! — обрадовался Нулик. — Ведь отдыхать после обеда можно и попивая кофе…

— Не ошибся, так скаламбурил, — сказал Сева.

— А симпозиум тоже, по-твоему, каламбур? — полюбопытствовал Нулик.

— Какой же это каламбур? — отозвался Олег. — Симпозиум — научное совещание в узком кругу специалистов.

— Ага! — кивнул Нулик. — Значит, это не каламбур, а шутка. Кому придёт в голову всерьёз называть специалистами Магистра, Единичку и мини-Джерамини Между прочим, славный парень этот Мини! Непременно приглашу его к нам в Карликанию.

— Между прочим, — передразнил Нулика Сева, — так мы никогда не доберёмся до задачи. Так что, будь любезен, сосредоточься и слушай, если ничего не можешь сказать сам. Мини, его сестра и их двоюродный брат провели на море в общей сложности год, с 1 января по 31 декабря. При этом Мини отдыхал в пять раз больше дней, чем двое других, вместе взятых. А если так, значит, число дней в году надо разделить на шесть частей. Без остатка на шесть разделится только год високосный, в котором 366 дней. Делим, стало быть, 366 на шесть и получаем 61. Вот сколько дней отдыхали родственники Мини. А так как сестра была на взморье на один день больше двоюродного брата, ясно, что пробыла она там 31 день, а двоюродный брат — 30 дней. Сам же Мини провёл на взморье в пять раз больше дней, чем они оба, то есть 305 дней.

— Не забудь, что Мини жил там без перерыва, — напомнила Таня, — и потому отдых его длился с 1 января по 31 октября включительно. А брату и сестре достались ноябрь и декабрь.

— Подумать только! — возмущался Нулик. — 305 дней в году! От такого отдыха устать можно!

— Философствовать потом будешь, — остановила его Таня. — Мы ещё должны узнать, сколько в то время было Мини лет…

— Нелепый вопрос!

— Очень даже лепый! Ведь отдыхал Мини в високосном году, а ближайший от нас минувший високосный год — 1968.

— А почему не 1964? — закапризничал Нулик.

— Да потому, что Мини сейчас всего пять лет, и в 1964 году его ещё на свете не было. Значит, отдыхал он на взморье в 1968 году, когда ему было три года.

— Значит, — сказал Сева, подражая Таниному голосу, — программа наша на сегодня исчерпана.

— Неужели все? — переспросил Нулик скорее испуганно, чем радостно.

— До капельки! — заверил его Сева. — Будьте благонадёжны!

Круглая физиономия президента вытянулась.

— А Магистра и Единички все нет…

Наступило тоскливое молчание. Больше делать было нечего, и время, как всегда в таких случаях, тянулось мучительно долго.