Владимир Левшин - Магистр Рассеянных Наук

Нулик грустно посмотрел на недоеденное пирожное.

— Ничего, старина! — утешил его Олег. — В конце концов, есть и решать задачу можно одновременно. В общем, Единичке нужно было разделить большой треугольный лоскут на пять небольших треугольников так, чтобы площади их относились, как 1:2:2:3:4.

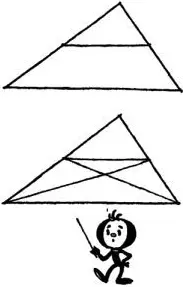
Он вынул карандаш и соединил середины боковых сторон треугольника, иначе говоря, провёл на салфетке одну из средних линий треугольника.

— Что у нас получилось? — спросил Олег. — Средняя линия разделила треугольник на две части. Одна из этих частей тоже треугольник, другая — трапеция. Все знают (а кто не знает, пусть докажет это сам), что площадь этого нового маленького треугольника в три раза меньше площади трапеции. Теперь проведём обе диагонали трапеции. Обратите внимание на то, что диагонали эти по совместительству представляют собой и медианы большого треугольника. Ведь они проведены в середине его боковых сторон! Все видят, что диагонали разделили трапецию на четыре части — на четыре треугольника. Самый маленький из них — верхний, два боковых — немного побольше, а самый большой — нижний. Узнаем, каковы площади этих треугольников.

— Узнаем! — решительно повторил Нулик, но тут же, впрочем, замолчал.

— Во-первых, нетрудно доказать (и пусть каждый опять-таки сделает это сам), что оба боковых треугольника равновелики, то есть имеют одинаковые площади. Во-вторых, приняв площадь самого маленького из этих четырех треугольников за единицу, выясним, во сколько раз каждый из остальных больше самого маленького.

Сева хлопнул себя по лбу.

— Стоп! Кажется, нашёл. Ведь медианы треугольника делятся в точке пересечения на части, которые относятся, как 1:2. Так? А так как высоты самого маленького треугольника и любого из боковых одинаковы, то площади их тоже относятся, как 1:2.

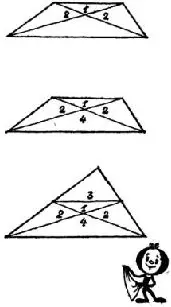
— Не в бровь, а в глаз! — констатировал Олег. — Большая часть задачи, таким образом, решена. Остаётся выяснить, во сколько раз площадь нижнего, самого большого треугольника больше площади самого маленького, принятого за единицу.

— И это тоже нетрудно! — подхватил Сева. — Ведь средняя линия, как известно, равна половине основания. А так как нижний и верхний треугольники, входящие в трапецию, подобны, то и высоты их тоже одна вдвое меньше другой. Ну, а раз так, то площади обоих треугольников относятся, как 1:4. Вот трапеция и разделилась на треугольники, площади которых относятся, как 1:2:2:4.

— Отлично! — сказал Олег. — Далеко пойдёте, молодой человек! А теперь ещё одно небольшое усилие: надо вспомнить, во сколько раз площадь первого отделённого нами треугольника меньше площади трапеции.

— Это я и без всяких усилий помню, — сказал Нулик. — Площадь отделённого треугольника меньше площади трапеции в три раза. Теперь подсчитаем, из скольких единиц состоит площадь трапеции. Площадь самого маленького мы приняли за единицу. Прибавим к этому два равных треугольника, площади которых вдвое больше, получим пять единиц. Теперь прибавим к этому площадь самого большого из четырех треугольников, равную четырём единицам. И получим всего девять единиц. Ну а 9, делённое на 3, опять-таки 3. Это и есть площадь первого отделённого нами треугольника.

— Молодчина! — одобрил Сева. — Теперь уж мы наверняка знаем, что площадь всего треугольника разделена на пять треугольников, площади которых относятся, как 1:2:2:3:4. Умница Единичка! Здорово решает задачи!

— Ура! — провозгласил президент и неожиданно, безо всякого перехода, похлопал себя по круглому пузику: — Ну и наелся же я!. Прямо как Пантагрюа и Гаргантюэль…

— Осади назад! — остановил его Сева. — С вашего позволения, не Пантагрюа и Гаргантюэль, а Гаргантюа и Пантагрюэль. Именно так называется книга Франсуа Рабле. Только читать тебе её, пожалуй, рановато. Всякому овощу…

Нулик только досадливо отмахнулся и очень недовольный вылез из-за стола. И то сказать: невелика радость, когда тебе на каждом шагу напоминают, что ты ещё маленький…

Удивительно быстро темнеет зимой! Когда мы вышли из кафе, на улицах уже зажглись фонари. Падал тихий, лёгкий снежок. Мы снова свернули в малолюдный переулок.

Нулик не выдержал, побежал. За ним принялись бегать остальные.

— Догоняй! — крикнула Таня, пробегая мимо президента.

Тот с весёлым визгом помчался за ней. Вот он уже почти касается её рукой… Вдруг Таня круто остановилась и подалась в сторону. В следующее мгновение президент растянулся на тротуаре.

— Это все она виновата! — жаловался он, потирая ушибленную коленку.

— Ничего, — сочувственно сказал Сева, — девчонки, брат, они все такие…

— Да нет, — неожиданно захихикал Нулик, — я не про Таню, а про центробежную силу.

И опять все грохнули.

— Нанялся ты, что ли, повторять Магистровы нелепицы? — недоумевал Сева. — Бежал по тротуару по прямой линии, потом неожиданно остановился и упал, — ну при чём тут, скажи на милость, центробежная сила?

— А при том, что если бы я бежал не с такой силой, я бы не упал.

— Эх, ты! Мыслитель! Центробежная сила проявляется только тогда, когда тело движется по кривой — ну, скажем, по кругу. Вот едешь ты, например, в такси, и водитель на полной скорости резко разворачивается. И валишься ты при этом набок. Прижимает тебя к боковой стенке машины.

— Или ещё, — вспомнила Таня. — Ты крутишь над головой камень, привязанный к верёвке. Крутишь все быстрей и быстрей, и верёвка при этом натягивается все больше и больше, как струна. И опять здесь виновата центробежная сила. А если ты уж слишком сильно раскрутишь верёвку, она может и разорваться.

— Понял, понял! — закричал Нулик. — Верёвка разорвётся потому, что камешек будет рваться прочь от центра. Отсюда, наверное, и название — центробежная сила! Так?

— Так, да не так, — сказал я.

Ребята удивлённо переглянулись.

— Понятие центробежной силы возникло в восемнадцатом веке. Ввёл его французский учёный д'Аламбер. Но силу эту он правильно назвал фиктивной, то есть воображаемой.

— Значит, на самом деле центробежной силы не существует?

— И да и нет. Д'Аламбер придумал это понятие для того, чтобы удобнее было изучать движение тела по кривой.

— Чепуха какая-то! — рассердился президент. — Сила воображаемая, а верёвку разорвала!

— Ну, это дело тонкое. В двух словах не объяснишь. Опять-таки — всякому овощу своё время. А что касается Магистра, то он просто-напросто забыл закон Ньютона. Забыл о том, что всякое тело стремится сохранить либо покой, либо прямолинейное равномерное движение. Это свойство тел называется инерцией. И когда Единичка, которая тянула Магистра за руку, внезапно остановилась, тот, все ещё продолжая двигаться по инерции, споткнулся и чуть было не упал.