Петр Путенихин - Диаграммы Пенроуза – что это такое?

В физике и математике практически невозможно обойтись без систем координат, которые всегда присутствуют в том или ином, явном или неявном виде. В литературе для наглядности во многих случаях используются их различные графические отображения . Несомненно, каждый, интересующийся этими науками, хорошо знаком, как минимум, с декартовыми координатами. Однако в процессе исследований часто появляется необходимость создания различных модификаций координатных систем, поскольку многие явления становятся более наглядными в своих собственных, специфических системах координат. Например, для величин, изменяющихся в широких диапазонах, были разработаны логарифмические системы координат, в которых по оси величина отображалась в виде её логарифма. Двойная логарифмическая координатная сетка, в частности, используется для демонстрации процесса расширения Вселенной после Большого Взрыва. Миллиардные величины расстояний в световых годах и времени в годах заменяются в этом случае шкалами в 15-20 единиц.

Некоторые другие процессы требуют еще более длительных интервалов, поэтому для них разработаны ещё более компактные шкалы. Например, в диаграммах Крускала-Шекереса, в которых применен "часовой принцип" отображения времени, напоминающего часовую стрелку, бесконечный интервал времени сжат в пределах прямого угла. Для этого угловая шкала сделана неравномерной: на её границах равномерные деления времени стремятся к бесконечно малым углам.

При описании космологических явлений, гипотез или решения тех или иных задач общей теории относительности, как можно заметить, чаще всего используются конформные диаграммы, разработанные одним из ведущих математиков и физиков – Роджером Пенроузом. Иногда в литературе указывается двойное авторство диаграмм – диаграммы Картера-Пенроуза. Конформным отображением является такое непрерывное отображение, преобразование координат, при котором сохраняются углы между кривыми и, соответственно, сохраняется форма бесконечно малых фигур.

В этих диаграммах использован все тот же принцип деформации координат. Они отображают пространственно- и времениподобные бесконечности на конечные расстояния, другим словами, отображают бесконечное пространство-время на квадрат конечных размеров.

Собственно говоря, это и является главным достоинством таких диаграмм – бесконечный диапазон изменения координат и изотропный характер светоподобных геодезических. Как в исходной диаграмме Минковского, так и на конформной диаграмме светоподобные геодезические имеют угол наклона ±45° и обозначают радиальные изотропные геодезические [1, с.139]. Это позволяет строить на диаграмме световые конусы и отслеживать поведение всех геодезических, выделяя среди них как времениподобные (вещественные тела), так и пространственноподобные (тахионы).

Следует отметить, что световые конусы на диаграммах на самом деле являются световыми треугольниками . На плоских диаграммах конус как таковой изобразить нельзя, а диаграммы с двумя пространственными координатами практически не рассматриваются. В случае светового треугольника все времениподобные геодезические в обязательном порядке должны находиться между сторонами треугольника, образованными двумя световыми лучами, и пересекать его основание t = const. Если же рассматривать трёхмерное пространство, то говорить также следовало бы не о световых конусах, а о световых сферах . В основе всех этих световых ограничителей лежит времениподобное уравнение интервала

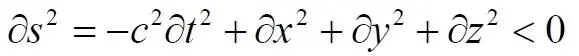
После тривиальных преобразований получаем

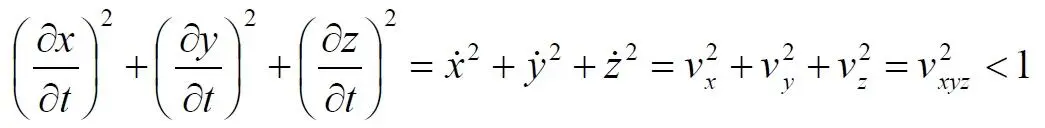
Уравнение означает, что скорость события всегда меньше скорости света c = 1. Графически уравнение тождественно поверхности (линии) касательных к геодезическим событий. Количество слагаемых в уравнении выбирается равным размерности пространства (не считая времени). Уравнение отражает обобщённое понятие светового конуса, то есть, и треугольника, и конуса, и сферы, и относится к геодезическим произвольной формы, к событиям, движущимся с ускорением.

Наименее очевидным является понятие световой сферы , относящейся к наиболее сложному случаю движения событий – одновременно по трём пространственным координатам. На трёхмерной диаграмме время, четвёртую координату непосредственно показать невозможно. Ситуацию позволяют разрешить динамические диаграммы. Это просто набор диаграмм, каждая из которых соответствует определённому моменту времени. Собственно координата времени в явном виде отсутствует и на такой диаграмме, анимации, но вместо неё можно показать световую сферу . В исследуемую точку траектории события помещается центр световой сферы и вектор скорости. Очевидно, направление его совпадает с траекторией, а длина равна скорости в этой точке. Световая сфера имеет радиус c = 1, поэтому вектор скорости не должен выходить за её пределы. Световая сфера охватывает все возможные направления движения события в данной точке, поэтому векторы скорости не являются мировыми линиями.

Следует отметить, что световой конус (треугольник) на диаграммах выполняет главным образом контрольную функцию. Он позволяет визуально определить времениподобный характер геодезических. Правда, непосредственно это относится к инерциальному движению. В случае ускоренного движения световой конус неявно относится не к самой геодезической, а к мысленно проведённой к ней касательной в исследуемой точке. Формально все световые ограничители можно заменить на обобщённый – световой вектор . Именно с ним и должен сравниваться вектор скорости события. На традиционных диаграммах Пенроуза мы мысленно, и, видимо, чаще всего неосознанно проводим единичную касательную к мировой линии события и также мысленно рассматриваем её проекцию на нулевую геодезическую. Если в этой исследуемой точке касательная совпадает с нулевой геодезической, то скорость события равна скорости света.

Можно заметить, что диаграмма Пенроуза-Картера чем-то похожа на диаграмму Крускала-Шекереса (Секереша) и для шварцшильдовской черной дыры не дает никакой принципиально новой информации.

В научных и научно-популярных статьях по физике, космологии можно заметить, что авторы часто при иллюстрации своих выкладок, доводов используют не совсем корректный приём. На приводимые иллюстрации они не наносят обозначения, поясняющие назначение или смысл изображенных на них элементов.