Игорь Житяев - Фотонно-стимулированные технологические процессы микро- и нанотехнологии

Анализ полученных результатов в области лазерных технологий показывает, что сдерживающим фактором при внедрении в промышленное производство применительно к микроэлектронике является недостаточная изученность физических процессов взаимодействия лазерного излучения с полупроводниковыми и пленочными структурами, отличающимися по своим оптическим и теплофизическим характеристикам. Кроме того, при лазерной обработке компонентов интегральных схем не всегда учитываются нелинейные параметры теплоемкости, теплопроводности, коэффициентов поглощения и отражения обрабатываемых структур, оказывающих существенное влияние на режимы обработки и воспроизводимость параметров технологического процесса. Сдерживающим фактором, несмотря на достигнутые успехи, является также недостаточный выбор источников лазерного излучения и отсутствие лазерного промышленного оборудования.

Успехи фотонных технологий были бы невозможны без достаточно развитой техники лазерного приборостроения и оборудования быстрой термической обработки полупроводниковых структур БИС, использующих некогерентные источники излучения.

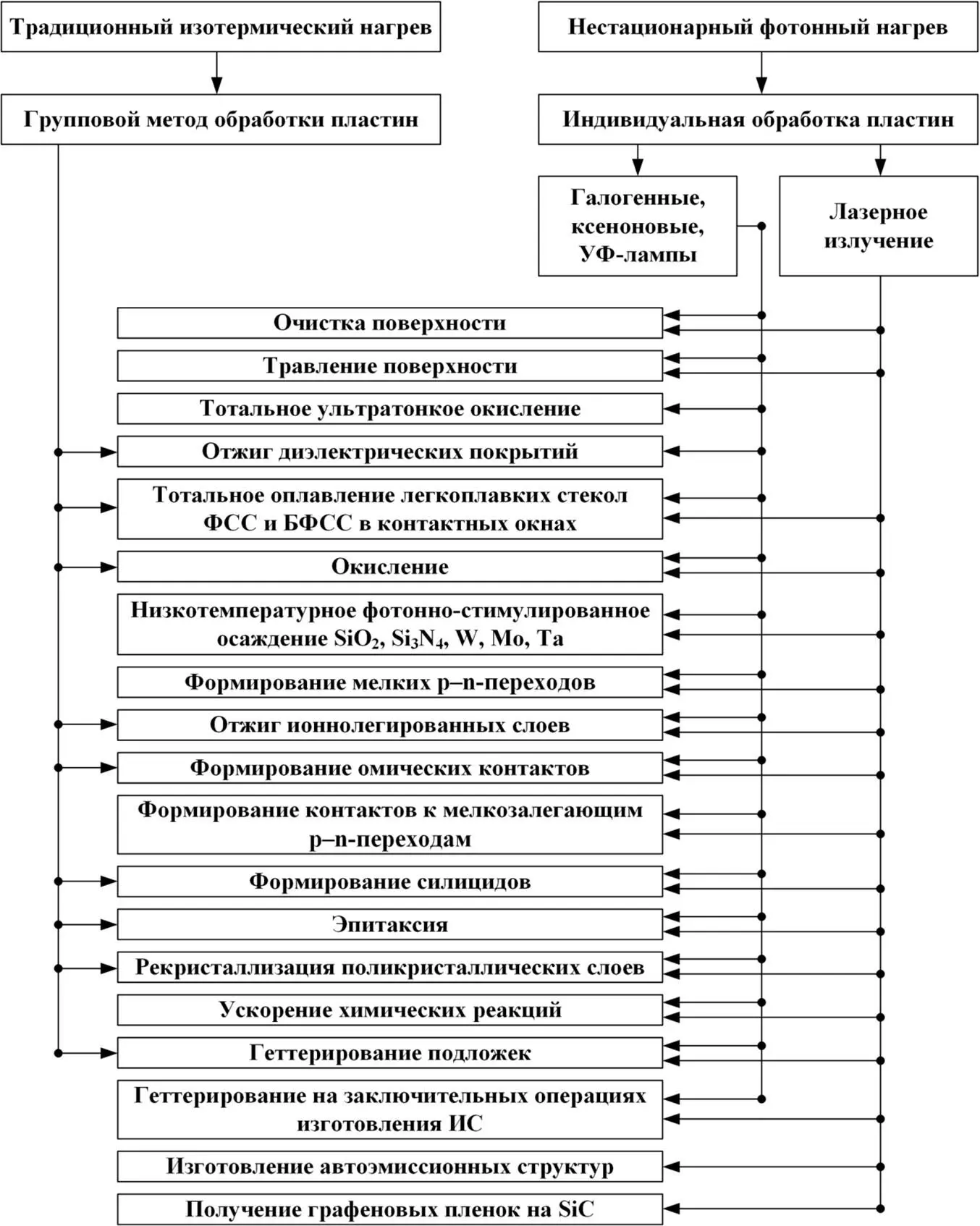
Рис. 1.Классификация традиционных и фотонно-стимулированных технологических процессов

Как известно, излучение, падающее на поверхность пластины, частично отражается, поглощается и может также пропускаться. Поэтому справедливо выражение для плотности потока излучения

где Р R, P A, P T– части плотности мощности потока облучения отраженного, поглощенного и пройденного сквозь пластину соответственно.

Первое слагаемое в правой части определяется коэффициентом отражения R S, второе и третье – коэффициентом поглощения и толщиной пластины.

Проникновение излучения в глубину твёрдого тела описывается законом Бугера – Ламберта

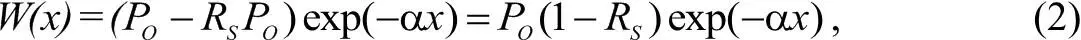
где α – коэффициент поглощения, x – координата по глубине. Тогда часть излучения, поглощенная пластиной толщиной d S , без учёта внутренних отражений будет равна

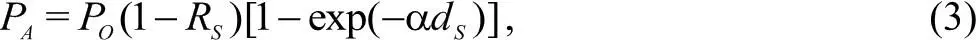
а выражение для плотности потока, прошедшего сквозь пластину, имеет вид

Уменьшение интенсивности фотонного излучения, проходящего через твёрдое тело, происходит за счёт взаимодействия с поглощающими центрами. Важнейшей оптической характеристикой облучаемой структуры является коэффициент поглощения.

В силу зависимости последнего от многих факторов (таких, как тип материала, концентрация легирующих примесей, дефектность структуры, температура, а также длина волны излучения) для адекватного моделирования рассматриваемых процессов необходим детальный анализ механизмов поглощения.

Полный коэффициент поглощения α равен сумме коэффициентов поглощения различными центрами:

В полупроводниках различают пять основных типов оптического поглощения:

– собственное;

– поглощение на свободных носителях;

– поглощение на локализованных состояниях;

– экситонное;

– решеточное [11, 12].

Световая волна, попадая в проводящую среду, воздействует на подвижные носители заряда. Электроны, ускоряясь, увеличивают свою энергию за счёт энергии волны. Сталкиваясь с решеткой, они отдают свою энергию решетке. Спектральная зависимость коэффициента поглощения свободными носителями заряда имеет вид

где е – заряд электрона; n , μ, m ef– концентрация, подвижность и эффективная масса носителей заряда соответственно; с – скорость света в вакууме; ε 0– диэлектрическая постоянная; 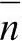– показатель преломления; λ – длина волны.

Если энергия фотонов больше ширины запрещённой зоны, то имеет место собственное поглощение, при котором электрон из валентной зоны может переходить в зону проводимости. При этом различают прямые и непрямые переходы электронов. В последних, характерных для кремния, наряду с фотоном и электроном участвует третья частица – фонон. Выражения для коэффициента собственного поглощения имеют вид

где hν – энергия фотона; E g– ширина запрещенной зоны; E P– энергия фонона; А – константа [11, 13].

Фотон может также поглощаться электроном или дыркой, находящейся в локализованном состоянии. При этом заряженная частица переходит либо в свободное, либо в другое локализованное состояние.

Локализованные состояния могут иметь различную физическую природу: атомы примеси в узлах или междоузлиях, вакансии и др. Поэтому в общем случае достаточно трудно получить выражение для коэффициента поглощения данного вида. Однако если локализованные состояния имеют водородоподобный спектр, то к ним можно применить теорию излучения (поглощения) атома водорода.

Тогда выражение для коэффициента поглощения на локализованных состояниях можно записать как

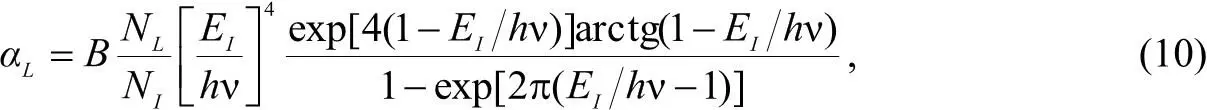
где N L,E I– концентрация и энергия ионизации рассеивающего центра; В – константа [11].

Входящие в (6-10) параметры E g, n, μ сами являются функциями многих переменных. В частности, ширина запрещенной зоны Е gс ростом температуры и концентрации примеси уменьшается. Наибольшее влияние E gна α проявляется в диапазоне температур 600-750 К из-за смещения края собственного поглощения в коротковолновую область.

Известная зависимость (11) для кремния не учитывает влияние дефектности и термохимических напряжений, однако они могут быть учтены с помощью коэффициента поглощения в локализованных состояниях [14].

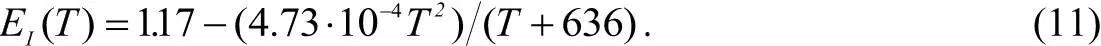
Концентрация свободных носителей заряда будет равна сумме собственной концентрации носителей n i, носителей, образованных ионизированными атомами примеси N I, и за счёт генерации неравновесных электронно-дырочных пар n g, поэтому справедливо будет выражение