Владимир Левшин - В поисках похищенной марки

Сева посмотрел на неё и тут же забраковал:

— В твоём питомнике будут вечные коммунальные склоки. Ведь однопородные собаки у тебя то и дело соседствуют! Например, в клетке четвёртого ряда снизу и четвёртого столбца слева сидит собака под номером 1. Но ведь наискосок от неё помещаются ещё две собаки под тем же номером. А как они реагируют на подобное соседство, ты знаешь.

Нулик только вздохнул и покорно принялся за поиски других вариантов. Ребята, каждый самостоятельно, занялись тем же. Правильное решение первым нашёл Олег. Он расположил собак по клеткам таким образом:

Нулик от этого варианта пришёл в восторг, но тут же попросил Олега сохранить его в тайне, чтобы о нём, упаси боже, не проведала Нуликова учительница.

Олег поглядел на него поверх очков:

— Это почему же?

— Понимаешь, — замялся президент, — если она узнает про этот фокус, так непременно воспользуется им на контрольных работах: составит четыре варианта задач и распределит их между нами в том же порядке, как ты рассадил собак. И пойдёт у нас собачья жизнь. Потому что никто ни у кого не сможет списывать.

До чего практический ребёнок!

— Вот заметят, что ты списываешь, — стращала Таня, — достанется тебе на орехи!

— Заметят? Ха-ха! Это ещё бабушка надвое сказала.

— Кстати, — спохватился Сева, — про бабушку-то мы и забыли. Давайте сосчитаем, сколько человек жило у Чёрного Льва вместе с бабушкой.

— Я уж давно сосчитал! — похвастался Нулик. — Вот следите: Чёрный Лев с женой — это двое, ещё две матери — уже четверо. Далее отец с сыном — шестеро. Дочка — это уж семь. Так? Затем бабушка с внуком — получается девять, да плюс зять с тёщей — итого одиннадцать человек как одна копеечка.

— А ещё президент! А ты не подумал, что бабушка — она ведь одновременно и мать и тёща, — улыбнулась Таня.

— А Чёрный Лев сразу и муж, и отец, и зять! — подхватил Сева.

— А жена его к тому же и мать и дочка! — продолжал Олег.

— Ну, а сын Чёрного Льва — внук своей бабушки! — закричал Нулик, включаясь в игру. — Так что у каждого из них по три звания. Кроме сына. У сына — всего два. Выходит, семейство Чёрного Льва состоит… дайте сосчитать… состоит из четырех человек. Так что пяти комнат им заглаза хватит, если, конечно, не считать собак.

— Что их считать! — отмахнулся Сева. — У собак есть свой собственный террариум. Давайте-ка поспешим на собачьи бега, а то они уже начались.

Тут все посмотрели на Пончика, который, соскучившись, бегал вокруг стола, как лошадь по манежу. Бутерброд с колбасой заставил его остановиться и прекратить свой цирковой номер.

— Дамы и господа, — провозгласил Нулик, — одни бега закончились, начинаются новые. На старте четыре рысака: пинчер под номером один, болонка под номером два, третий номер у спаниеля, четвёртый — у таксы. Приготовились, внимание, старт! А теперь вы решайте задачу, а я чуток отдохну.

Сева погрозил ему кулаком:

— Пользуешься тем, что мы гости воспитанные и не можем тебе ответить как следует?

— Пока вы пререкаетесь, собаки давно уже поравнялись, — сказал Олег, протягивая бумажку. — Вот вам моментальная съёмка бега. По ней вы можете легко убедиться, что все четыре собаки встретились в первый раз на расстоянии двух третей дорожки. Если, конечно, считать от старта.

— Ха! — Нулик язвительно усмехнулся. — Такую фотографию и я сделаю. Только у меня собаки встретятся на трех четвертях дорожки, считая от старта, а у Севы на семи девятых… Нет, ты мне доказательства подавай!

— Устами младенца глаголет истина, — поддакнул Сева.

— Какая там истина! — огрызнулась Таня. — Уж если Олег говорит две трети, значит, две трети!

Но Нулик был неумолим:

— Пусть докажет.

И Олег стал доказывать:

— Рассмотрим сперва бег двух собак: таксы, которая бежит медленнее всех, и спаниеля. Спаниель бежит вдвое быстрее таксы. Ясно, что он с самого начала её опередит и потому встретится с нею только на обратном пути. Обозначим теперь через икс путь, пройденный таксой до встречи со спаниелем, а длину беговой дорожки — буквой a . В таком случае спаниель до встречи с таксой пройдёт путь, равный a + a - x , то есть 2 a - x . На этой бумажке изображён момент их встречи.

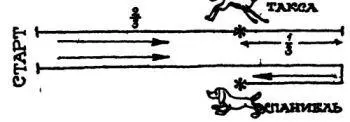
— Пока все правильно, — заметил Нулик. — Посмотрим, что будет дальше.

— А дальше, — продолжал Олег, — примем скорость таксы за единицу. Тогда скорость спаниеля будет равна двум. Спрашивается, сколько времени потратит такса, чтобы встретиться со своим соперником?

— Ясно, икс секунд, — заявил президент.

— А может, быть, и минут, — поправил Олег, — но это неважно. Ну, а спаниель потратит на свой путь вдвое меньше времени, то есть

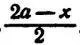
Остаётся оба выражения приравнять между собой — ведь собаки-то встретились!

— Приравняем, — согласился Нулик. — Получим…

— Мы пахали, — в тон ему сказала Таня.

— Получим, что

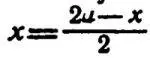
— невозмутимо продолжал Олег.

— А отсюда любой школьник найдёт, что… Что он найдёт?

— Он найдёт, что 2 x =2 a - x . Откуда 3 x =2 a , а уж один икс равен двум третям a. x = 2/ 3 a , — закончил Олег. — Именно это я и сфотографировал.

— Принимается! — внушительно изрёк Нулик. — Но где же другие собаки?

— Будут тебе и другие. Рассуждаю так: за то время, что такса одолела 2/ 3дорожки, болонка, которая бежит в четыре раза быстрее таксы, пройдёт 8/ 3пути, то есть 2 2/ 3 a . Иначе говоря, болонка успела пробежать дважды дорожку, да ещё 2/ 3её и, следовательно, тоже поравнялась и с таксой, и со спаниелем.

— Блеск!.. — закричал Нулик. — Давай дальше!

— А дальше остаётся самый быстроходный пёс — карликовый пинчер. Он бежит в восемь раз быстрее таксы и сумел за то же время, что и она, пробежать путь, равный 16/ 3 a , то есть 5 1/ 3 a . Значит, пробежав беговую дорожку пять раз, пинчер на шестом разе, идя навстречу таксе, пробежал ещё 1/ 3 a . Итак, все собаки встретились одновременно. А вот и схема бега:

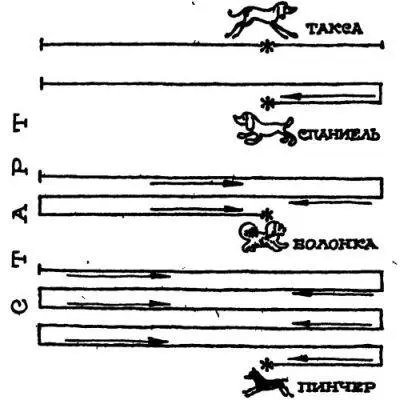
Но Нулик все ещё переходил от восторга к сомнению:

— Пока что все правильно. Но что же дальше? Когда собаки встретятся во второй раз, и в третий, и в двадцатый?