Владимир Левшин - Фрегат капитана Единицы

У правильной дроби числитель всегда меньше знаменателя, а у неправильной — больше.

Значит, есть дроби, которые больше единицы? Да, есть. Если разделить пять на два, получится неправильная дробь 5/ 2 — пять вторых. А это всё равно что два с половиной, и записывается так: 2 1/ 2. Вот и выходит, что неправильная дробь больше единицы.

— А теперь, — сказал капитан, — посмотрите направо. Перед вами Залив Десятичных Дробей.

Да, оказывается, есть и такие дроби. Это те, у которых знаменатель всегда либо десять, либо сто, либо тысяча… Словом, число, которое делится на десять без остатка.

Коку это очень понравилось, и он заявил, что теперь будет бить чашки только на десятичные осколки.

— А записывать это буду так, — добавил он,

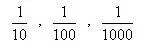
Верно?

— И верно, и неверно, — ответил капитан. — Десятичные дроби принято записывать иначе, в строчку. Если число больше единицы, целую часть его отделяют от дробной запятой. А если число меньше единицы, то перед запятой ставят нуль.

— А где же пишут знаменатель? — спросил я.

— Знаменателя совсем не пишут, — ответил капитан, — его подразумевают. Дело в том, что у десятичных дробей, как и у целых чисел, есть разряды. Первый знак после запятой справа указывает, сколько десятых долей в числе, второй — сколько сотых, третий — сколько тысячных, и так далее. Вот, например, 0,2 читается так: две десятых. А 0,02 — две сотых…

Под конец капитан попросил нас прочитать такое число: 0,023.

Я ответил, что это очень легко: нуль целых, нуль десятых, две сотых и три тысячных. Капитан страшно удивился:

— Зачем же читать по складам, когда можно сразу: двадцать три тысячных. Если после запятой число состоит из трёх цифр, значит, подразумевается, что это число надо разделить на тысячу. Вот и всё. А теперь идите-ка чистить картошку.

Мы с коком уселись на корме и принялись за дело. Трудиться здесь приходится вовсю.

Неожиданно похолодало, пошёл снег. Он лез в глаза, мешал работать, и я решил подождать, пока он кончится.

Вдруг — тррррррах! Гром. Один удар, другой, третий… Сверкают молнии. А снег всё идёт. Снег и гроза? Невероятно!!

— А что значит невероятно? — спросил кок.

— Невероятно, — пояснил я, — это когда совсем невозможно.

— Как же невозможно, когда гремит? — засмеялся Пи.

— Это просто случайно. А вообще не бывает.

Тут появился капитан и сказал, что я неправ. Всё, что может произойти даже случайно, — всё вероятно. Только иной раз приходится этого очень долго ждать. Тогда говорят, что для такого случая вероятность мала.

— Значит, вероятность можно измерить? — удивился я.

— Конечно. На то и появилась математическая наука — теория вероятностей. Кстати, острова, мимо которых мы идём, принадлежат архипелагу Вероятностей.

— Что ещё за архипелаг? — спросил я.

— Ах да, я и забыл, что вы ещё этого не знаете, — улыбнулся капитан. Архипелагом называется скопление островов.

Снег кончился, и Фрегат пришвартовался к острову, на флаге которого красовалась дробь 1/ 2— одна вторая, иначе говоря — половина. Какой-то половинчатый остров!

Жители встретили нас приветливо, но мне почудилось, что им не до гостей. Оказалось, что все они играют в шахматы, и даже не играют, а только бросают жребий, кому играть белыми! Один зажмёт в каждом кулаке по фигуре и предлагает приятелю угадать: где белая? И оба радуются, когда угадывают.

Капитан попросил игроков дать и ему две пешки: зажал каждую в кулаке и спросил кока: в какой чёрная? Тот ответил: в правой, но ошибся. Тогда я сразу отгадал, что чёрная в левой руке, и решил, что игра пустяковая. Но капитан сказал, что вовсе не пустяковая.

— Дело в том, — продолжал он, — что на этом острове отгадывают цвет шахматных пешек. Но так как их всего два — чёрный и белый, — а угадать надо только один из двух, то и говорят, что вероятность угадывания равна отношению одного к двум, то есть 1/ 2. Вот почему на флаге этого острова написана эта дробь. А если бы перед нами было не две, а несколько разноцветных пешек — красная, зелёная, синяя, жёлтая и так далее, то угадать, какая из них зажата в руке, было бы уже гораздо труднее. В этом случае вероятность угадывания уменьшается.

И капитан повёз нас на остров, обозначенный дробью одна шестая: 1/ 6. Жители его играли в кости. У игроков были костяные чёрные кубики. На каждой из его шести сторон нарисованы белые точки: на одной стороне — одна, на другой — две, и так до шести. Точки эти называются очками. Один игрок подбросит кубик, а другой загадывает, сколько выпадет очков.

Понятно, что угадывали на этом острове гораздо реже, чем на первом. И я догадался, что вероятность угадывания здесь равна отношению одного к шести, то есть 1/ 6.

— Верно, — сказал капитан и спросил, какова будет вероятность угадывания, если задумать, чтобы выпало либо два очка, либо четыре.

И я опять догадался, что тогда и вероятность станет вдвое большей. Она будет равна уже не 1/ 6, a 2/ 6. А это всё равно что одна треть — 1/ 3.

— А вот что будет, если задумать, чтобы выпало ЛЮБОЕ число очков?

— Тогда нужно ехать на другой остров, — ответил капитан, — на остров Достоверностей. Вон тот, с синим флагом.

Только теперь я заметил синий флаг, на котором красовалась не дробь, а единица. Это почему же?

— Да потому, — пояснил капитан, — что тебе нужно, чтобы из шести возможных случаев выпал любой. Значит, вероятность угадывания равна отношению шести к шести: 6/ 6— стало быть, единице. А это уже достоверность, то есть то, что произойдёт непременно.

В это время кок заметил остров, над которым развевался чёрный флаг с большим белым нулём посередине. Капитан сказал, что это остров Невероятностей, то есть остров, где вероятность угадывания равна нулю.

— Как же это может быть? — спросили мы с коком одновременно.

— А вот как, — ответил капитан. — Предположим, кто-нибудь из вас загадает, чтобы у этого кубика выпало СЕМЬ очков.

— Но это невозможно! — воскликнул я. — Ведь у кубика cамое большое число очков — шесть.

— В том-то и дело, — обрадовался капитан. — Стало быть, семь выпасть не может. Значит, в этом случае нет никакой вероятности, что вы отгадаете. Вероятность равна нулю!

Интересная игра — теория вероятностей! Но капитан возмутился и сказал, что это не игра, а наука. Хотя и родилась она из игры. Так частенько бывает. И ещё он сказал, что теория вероятностей помогает учёным, инженерам и особенно экономистам, что она необходима народному хозяйству страны и что мы в этом очень скоро убедимся.