Владимир Левшин - Черная маска из Аль-Джебры

Мы, во всяком случае, испытание выдержали: нас благополучно выдуло наружу. Сам понимаешь, как все обрадовались, когда очутились наверху.

Сперва глаза наши ничего не различали и только щурились от утреннего солнца. Но потом…

Не хочется тебя разочаровывать, но потом они тоже ничего особенного не увидели. Мы даже подумали, что в темноте незаметно перепутали направление и вернулись обратно в Карликанию. Перед нами была дорога, очень похожая на ту, что ведет из Арабеллы к подземелью.

Но тут Сева (ты ведь знаешь, как он любит читать вывески!) задрал голову и прочитал:

Тогда и мы с Таней увидали эту странную надпись. Громадные разноцветные буквы выгнулись радугой прямо в воздухе, приглашая в какую-то непонятную Аль-Джебру. Что за Аль-Джебра? Город она? Или целая страна? И как мы пойдем туда без волшебного талисмана?

И досталось же ему, бедняге! Не очень-то вежливо мы о нем говорили. И зря: все это время стручок преспокойно лежал у меня в кармане. До чего ж я обрадовался, когда нащупал его там вместе с шифрованной запиской!

Теперь можно бы подумать о Черной Маске и начать поиски. Но где Пончик? Мы долго звали его, обшарили все кусты — напрасно. Как сквозь землю провалился! Сева и впрямь уверял, что Пончик остался в подземелье, и чуть не уговорил нас идти обратно.

Но только мы повернули, стручок в моем кармане беспокойно заерзал, а когда я попытался его успокоить, уколол мне ладонь острым хвостиком. Похоже, что предложение Севы ему не понравилось и он не прочь снова удрать. Как тут быть?

Посовещавшись, двинулись дальше. И правильно сделали. Потому что стручок сейчас же успокоился. Он будто знал, что не пройдет и пяти минут, как Пончик вынырнет из какого-то овражка и бросится нас облизывать.

Как видишь, Нулик, тебе беспокоиться нечего. Сейчас твой почтальон помчится выполнять свое первое поручение. А пока — до свидания. Все тебе кланяются.

Олег.

Привет, Нулик! Ты, конечно, ждешь, что я тебе сразу расскажу про Черную Маску. Но мы пока о ней ничего не узнали. Как говорится, никаких следов не обнаружено.

Вообще тайнами здесь и не пахнет. Оказывается, Карликания и Аль-Джебра — дружественные государства.

Удивляюсь, как ты этого не знал? Тут я срисовал для тебя один документ. Такие в Аль-Джебре висят чуть ли не на каждом столбе.

Вот, полюбуйся:

А что там дальше, я списывать не стал. На это надо весь день потратить. Я бы и недели не пожалел, если бы все это имело хоть какое-нибудь отношение к Черной Маске. Но, скажи на милость, при чем тут Черная Маска?

На каждом шагу натыкаешься на карликан: разгуливают себе почем зря целыми пачками. Многие здесь и живут.

Только что мы побывали в одном карликанском поселке с ужасно смешным названием — Обжоры. Таня вспомнила, что у нас есть город Ижоры. Я не поверил. Тогда она прочитала стихотворение Пушкина «Подъезжая под Ижоры». То есть не все стихотворение, а только первые четыре строчки. Но и это, по-моему, лишнее: мы-то ведь попали не в Ижоры, а в Обжоры. Так что нечего хвастаться своей образованностью.

В Обжорах и впрямь живут страшные лакомки: все они без конца что-то жуют.

В поселке только одна улица, но каждая ее сторона имеет свое название: «Обжоры среднеарифметические» и «Обжоры среднегеометрические».

Сначала я не обратил на это внимания. Но оказалось, что между жителями двух сторон большая разница, хоть и те и другие одинаково зазывали нас в гости.

Ну, мы порядком проголодались и отказываться не стали.

Пошли сначала к обжорам среднеарифметическим. И здорово прогадали. Ничем, кроме разговоров, нас не угостили. Под конец им, правда, неудобно стало, и они рассказали, в чем дело.

Все жители у них, ясное дело, работают. Кто лучше, кто хуже, кто больше наработает, кто меньше. Но они на это не смотрят: складывают все вместе, а потом делят на всех поровну. У одного, например, на грядке выросло четыре килограмма огурцов, а у другого — девять. Сумма этих чисел равна тринадцати. Тринадцать делят на два. Вот каждый и получает по шести с половиной килограммов огурцов. Конечно, обжор-то не два, а гораздо больше. Но сколько бы их ни было, они складывают все, что наработали, сумму делят на число работников, и каждый съедает свою долю до крошки. Где уж тут гостей кормить! Могли бы, правда, оставить кое-что про запас, так нет! На то они и обжоры.

После такого приема не очень-то хотелось идти к обжорам среднегеометрическим. Но мы все-таки пошли, и на этот раз нас накормили на славу!

Мы никак не могли понять, в чем дело.

— Может быть, — спрашиваем, — у вас делят не поровну?

— Нет, — говорят, — тоже поровну.

— Так, может быть, — спрашиваем, — вы не обжоры?

— Нет, — говорят, — обжоры.

— Откуда же у вас такие запасы?

Тут они нам и объяснили. Дело в том, что собранные продукты они не складывают, а перемножают. То есть не продукты, конечно, а количество их.

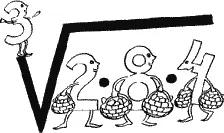
Один, скажем, снял с грядки четыре килограмма огурцов, а другой опять-таки девять:

Ты, наверное, думаешь, что тридцать шесть надо разделить на два? А вот и нет. Обжоры среднегеометрические и тут поступают по-своему. Они не делят, а извлекают из полученного произведения корень. Да, да, не удивляйся: у чисел есть корни и их можно извлекать. Об этом нам еще в прошлый раз рассказала Тройка с чемоданчиком на Проспекте действующих знаков. Эти самые знаки высыпались у нее из чемоданчика прямо на тротуар.

Помножь три на три. Получится девять. Знаешь, что ты сделал? Ты возвел три во вторую степень. Если же ты хочешь возвести три в третью степень, помножь его само на себя три раза. Получится двадцать семь. Пятая степень трех будет уже двести сорок три…

Так можно возвести число и в сотую, и в двухсотую, и в какую хочешь степень.

А теперь ответь на такой вопрос: какое число нужно возвести во вторую степень, чтобы получить девять? Разумеется, три. Вот это три и есть корень второй степени из девяти.

Стало быть, извлечение корня — действие обратное возведению в степень. Совсем как вычитание — действие обратное сложению, а деление — умножению.

Так вот, из числа тридцать шесть среднегеометрические обжоры извлекают корень квадратный, иначе говоря, корень второй степени. Получается шесть.

Выходит, каждому обжоре досталось по шести килограммов огурцов. Это немного меньше, чем получил бы обжора среднеарифметический. Но зато при такой дележке один килограмм остается в запасе.