Вячеслав Бодров - Психология профессиональной пригодности

Расчет коэффициента ассоциации

Рассмотрим пример вычисления коэффициента ассоциации при изучении связи между такими критериями пригодности, как I и IV группы, и критериями успешности обучения – лучшие и отчисленные:

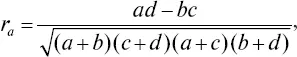
где a, b, c, d – численности альтернативных признаков (практически неограничены).

В корреляционной решетке (табл. 10) приведены исходные данные для расчетов ( x – группа; y – успешность обучения).

Подставляя в формулу соответствующие значения из таблицы, находим величину коэффициента ассоциации ( r a= 0,65), который выражается в долях от 0 до 1. Достоверность оценивается по его отношению к средней ошибке, определяемой по формуле

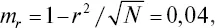
откуда t = 16,25.

Достоверность r aможет быть определена также и по специальным таблицам [52].

При изучении корреляционной зависимости между вариационными рядами с отсутствием линейной зависимости более правомерным является вычисление корреляционного отношения, которое измеряет состояние любых, в том числе и нелинейных, связей между признаками.

В отличие от коэффициента корреляции, изучающего двустороннюю связь между x и y , корреляционное отношение (η) показывает только зависимость изменений второго ( y ) признака от изменений первого ( x ), или наоборот. Корреляционное отношение – величина относительная, положительная и принимает значение от 0 до 1. Показатели корреляционного отношения обычно не равны между собой – η y/x≠ η x/y. Они определяются по следующим формулам

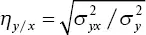
и

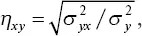
где

Эти формулы можно выразить и в другом виде:

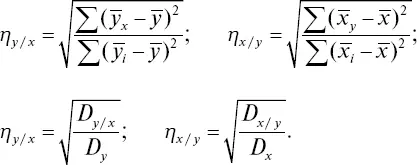
По приведенным формулам удобно определять коэффициенты корреляционного отношения для небольших выборок, а при наличии большого числа наблюдений необходимо предварительно весь материал группировать в вариационные ряды и вносить в корреляционную таблицу.

Рассмотрим вычисление корреляционного отношения на выборке из 10 наблюдений (табл. 11).

Таблица 11

Вычисление корреляционного отношения

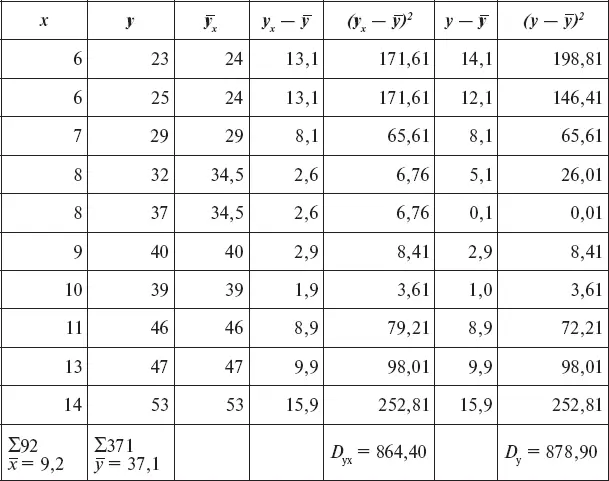
Сначала находим коэффициент корреляционного отношения полетов y по грубым ошибкам x , то есть η y/x, для чего ранжируем выборку по x (значения x расположены в возрастающем порядке сверху вниз). Затем определяем вспомогательные величины для вычисления корреляционного отношения по x и подставляем в формулу, откуда η y/x= 0,99.

Таким же способном определяем корреляционные отношения грубых ошибок x по полетам y , ранжируя выборку по y и определяем η y/x.

Для оценки достоверности полученных величин используем формулу

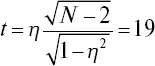
и по специальной таблице [52] находим значение P = 99,9 %.

Вычисление корреляционного отношения на больших выборках после предварительного заполнения корреляционной решетки можно производить по способу произведений, способу условных средних и способу суммирования [141].

Регрессионный анализ. Описанные показатели корреляции позволяют измерять степень связи, направление и форму существующей между ними зависимости. Однако они не дают информации о том, насколько в среднем может измениться в ту или другую сторону один из признаков при изменении другого. Такая информация представляет большой практический интерес для разработки методик психологического отбора, а также изучения влияния специальных методов подготовки на успешность профессионального обучения.

Функция, позволяющая по величине одного признака ( x ) находить средние (ожидаемые) значения другого признака 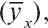связанного с x корреляционно, называется регрессией, а статистический анализ регрессии получил название регрессионного.

Важную роль в регрессионном анализе играет коэффициент регрессии ( R ), являющийся не только параметром уравнения, но и мерой регрессии y по x и x по y . Показатели его величины ( n ) характеризуют зависимость между переменными x и y по их абсолютным значениям, а показатели корреляции – величины относительные и измеряют тесноту связи между признаками в долях единицы. Коэффициент регрессии характеризует только линейную связь, при которой увеличения (уменьшения) одной переменной – y – пропорциональны увеличениям другой – x , и в зависимости от направления связь либо положительна, либо отрицательна. По значениям R легко определяется коэффициент корреляции 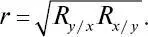Зависимость между R и r позволяет контролировать правильность расчета этих показателей, а также находить неизвестную величину одного из них по известной другой. Кроме того, при помощи регрессионного анализа можно исследовать корреляционную зависимость между признаками при малых выборках, но при этом необходимо помнить, что полученные коэффициенты могут оказаться несколько завышенными.

Коэффициент регрессии позволяет рассчитать, насколько в среднем изменится признак при изменении на единицу меры другого связанного с ним признака. Он рассчитывается по коэффициентам корреляции и средним квадратическим отклонениям сопряженных видов по следующим формулам:

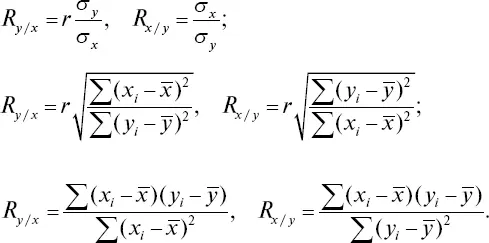
По формулам R y/xопределяется среднее (ожидаемое) значение y при изменении на единицу меры х, а по формулам R x/yнаходят среднюю величину х при изменении на единицу меры признака у.

Имея возможность легко менять условия проведения эксперимента по методике у и быстро оценивать полученные результаты, мы можем установить необходимые или оптимальные условия для другой методики x – более сложной и трудоемкой. Зная интеркорреляционные связи между методиками «батареи» тестов и проводя регрессионный анализ, можно добиться оптимальных и наиболее целесообразных условий их проведения и соответственно повысить прогностичность «батареи» в целом. Например, коэффициент корреляции между результатами обследования по методике y (время – с.) и x (количество ошибок) равен +0,25; σ y= 27, σ x= 5. Подставляя значения в формулу, находим R y/x= 1,35 и R x/y= 0,995. Это означает, что увеличение времени выполнения на 1 сек соответствует увеличению количества ошибок в среднем на 0,05 ошибок, а увеличение на одну ошибку при выполнении задания соответствует увеличению времени чтения таблицы на 1,35 с.