Яков Перельман - Занимательные опыты и задачи по физике

Рис. 98.Такие часы имеет при себе двойник, которого вы видите в зеркале.

Наконец, у вашего зеркального двойника есть физический недостаток, от которого вы, надо думать, свободны: он левша. Он пишет, шьет, ест левой рукой, и если вы выразите готовность с ним поздороваться, он протянет вам левую руку.

Нелегко решить, грамотен ли ваш двойник. Во всяком случае грамотен как-то по особенному. Едва ли удастся вам прочесть хоть одну строку из той книги, которую он держит, или какое-нибудь слово в тех каракулях, которые он выводит своей левой рукой.

Таков тот человек, который притязает на полное сходство с вами! А вы хотите судить по нему о внешнем виде вас самих…

Шутки в сторону: если вы думаете, что, глядя в зеркало, видите самих себя, – вы заблуждаетесь. Лицо, туловище и одежда у большинства людей не строго симметричны (хотя мы этого обычно не замечаем): правая половина не вполне сходна с левой. В зеркале все особенности правой половины переходят к левой, и наоборот, так что перед нами является фигура, производящая зачастую совсем иное впечатление, чем наша собственная.

Нетождественность зеркального отражения с оригиналом еще заметнее выступает в следующем опыте.

Поставьте перед собой отвесно на стол зеркало, положите перед ним бумажку и попробуйте нарисовать на ней какую-нибудь фигуру, например прямоугольник с диагоналями. Но не смотрите при этом прямо на свою руку, а следите лишь за движениями руки, отраженной в зеркале.

Вы убедитесь, что столь легкая на вид задача почти невыполнима. В течение многих лет наши зрительные впечатления и двигательные ощущения успели прийти в определенное соответствие. Зеркало нарушает эту связь, так как представляет глазам движения нашей руки в искаженном виде. Давнишние привычки будут протестовать против каждого вашего движения: вы хотите провести линию вправо, а рука тянет влево, и т. п.

Рис. 99.Рисование перед зеркалом.

Еще больше неожиданных странностей вы встретите, если вместо простого чертежа попробуете рисовать перед зеркалом более сложные фигуры или писать что-нибудь, глядя на строки в зеркале: выйдет комичная путаница!

Те отпечатки, которые получаются на пропускной бумаге, – тоже изображения зеркально симметричные. Рассмотрите надписи, испещряющие вашу пропускную бумагу, и попробуйте прочесть их. Вам не разобрать ни одного слова, даже вполне отчетливого: буквы имеют необычный наклон влево, а главное, последовательность штрихов в них не та, к какой вы привыкли. Но приставьте к бумаге зеркало под прямым углом – и вы увидите в нем все буквы написанными так, как вы привыкли их видеть. Зеркало дает симметричное отражение того, что само является симметричным изображением обыкновенного письма.

Мы знаем, что в однородной среде свет распространяется прямолинейно, т. е. скорейшим путем. Но свет избирает скорейший путь также и в том случае, когда не идет от одной точки к другой непосредственно, а достигает ее, предварительно отразившись от зеркала.

Проследим за его путем. Пусть буква A на рис. 100 обозначает источник света, линия MN – зеркало, а линия АВС – путь луча от свечи до глаза C . Прямая KB перпендикулярна к MN .

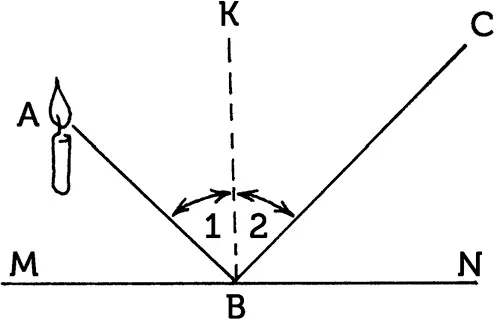
Рис. 100.Угол отражения 2равен углу падения 1.

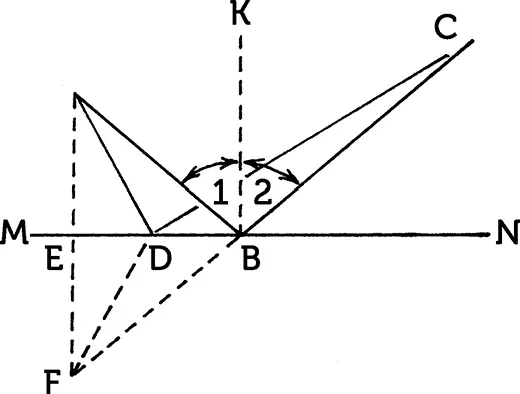
Рис. 101.Свет, отражаясь, избирает кратчайший путь.

По законам оптики угол отражения 2 равен углу падения 1 . Зная это, легко доказать, что из всех возможных путей от A к C , с попутным достижением зеркала MN , путь АВС – самый скорый. Для этого сравним путь луча АВС с каким-нибудь другим, например с ADC (рис. 101). Опустим перпендикуляр АЕ из точки A на MN и продолжим его далее до пересечения с продолжением луча ВС в точке F . Соединим также точки F и D . Убедимся, прежде всего, в равенстве треугольников ABE и EBF . Они – прямоугольные, и у них общий катет ЕВ ; кроме того, углы EFB и ЕАВ равны между собой, так как соответственно равны углам 2 и 1 . Следовательно, AE = EF . Отсюда вытекает равенство прямоугольных треугольников AED и EDF по двум катетам и, следовательно, равенство AD и DF .

Ввиду этого мы можем путь АВС заменить равным ему путем CBF (так как AB = FB ), a путь ADC – путем CDF . Сравнивая же между собой длины CBF и CDF , видим, что прямая линия CBF короче ломаной CDF . Отсюда путь АВС короче ADC , что и требовалось доказать!

Где бы ни находилась точка D , путь АВС всегда будет короче пути ADC , если только угол отражения равен углу падения. Значит, свет действительно избирает самый короткий и самый скорый путь из всех возможных между источником, зеркалом и глазом. На это обстоятельство впервые указал еще Герон Александрийский, замечательный греческий механик и математик II века.

Уменье находить кратчайший путь в случаях, подобных сейчас рассмотренным, может пригодиться для решения некоторых головоломок. Вот пример одной из таких задач.

На ветке дерева сидит ворона. Внизу на дворе рассыпаны зерна. Ворона спускается с ветки, схватывает зерно и садится на забор. Спрашивается, где должна она схватить зерно, чтобы путь ее был кратчайшим (рис. 102).

Рис. 102.Задача о вороне. Найти кратчайший путь до забора.

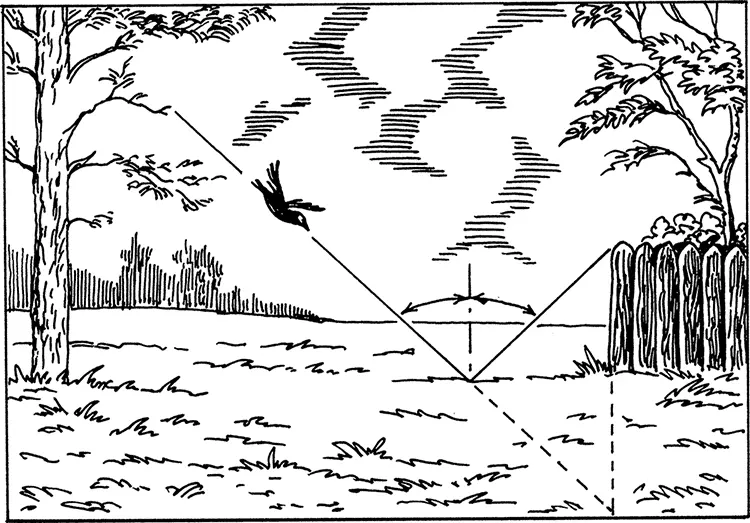
Рис. 103.Решение задачи о вороне.

Задача эта совершенно сходна с той, которую мы только что рассмотрели. Нетрудно поэтому дать правильный ответ: ворона должна подражать лучу света, т. е. лететь так, чтобы угол 1 был равен углу 2 (рис. 103). Мы уже видели, что в таком случае путь оказывается кратчайшим.

Всем известна хорошая игрушка, носящая название калейдоскопа: горсточка пестрых осколков отражается в двух или трех плоских зеркальцах и образует удивительно красивые фигуры, разнообразно меняющиеся при малейшем повороте калейдоскопа. Хотя калейдоскоп довольно общеизвестен, мало кто подозревает, какое огромное число разнообразных фигур можно получить с его помощью. Допустим, вы держите в руках калейдоскоп с 20 стеклышками и 10 раз в минуту поворачиваете его, чтобы получить новое расположение отражающихся стеклышек. Сколько времени понадобится вам, чтобы пересмотреть все получающиеся при этом фигуры?