Александр Челноков - Общая и прикладная экология

Выделяют три основных типа поведения кривой относительного доминирования, соответствующих различным типам взаимодействий между видами в сообществе.

Кривая 1 отвечает ситуации, когда члены сообщества находятся в сильной зависимости от некоторого ресурса, распределенного вдоль одномерного континуума, причем имеет место случайное, но без пересечений распределение частных ниш видов вдоль координатной оси данного ресурса (модель разломанного стержня Р. Мак-Артура). Показатель значимости в этом случае ведет себя в соответствии с формулой

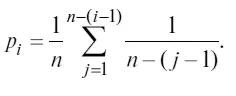
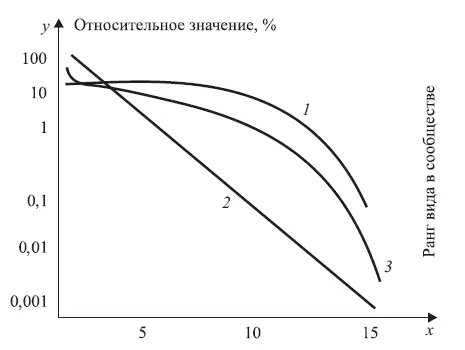
Рис. 1.7. Кривые относительного доминирования – разнообразия

Подобный тип рангового распределения наиболее часто встречается в немногочисленных по числу видов группировках таксономически близких животных в четко ограниченных однородных биоценозах (например, группировка птиц, гнездящихся на ограниченном участке леса). Также это справедливо для высших животных с активной конкуренцией, устойчивой численностью и высокой продолжительностью жизни.

Кривая 2 , представляющая собой прямую, изображает случай так называемого геометрического распределения и соответствует следующей схеме относительного доминирования: первый вид занимает половину доступного пространства существующих экологических ниш, второй – половину оставшегося пространства (25 % исходного) и т. д. В более общем случае существует фиксированное число с (0 ≤ с ≥ 1):

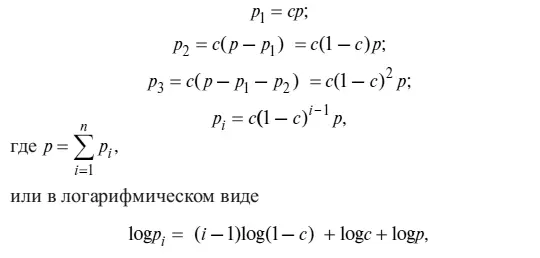
откуда видно, что величина p i как функция ранга i изображается на полулогарифмической шкале прямой линией с угловым коэффициентом log (1 – c ).

Геометрическое распределение относительного доминирования обнаруживается в группировках, состоящих из небольшого числа видов, которые находятся в жесткой конкуренции за ограниченные ресурсы, нередко в суровых условиях внешней среды.

Получаемую круто падающую прямую 2 можно рассматривать в качестве альтернативы для относительно пологой кривой 1 , соответствующей распределению Мак-Артура.

Эти две кривые представляют крайние случаи истории биоценоза. Обычно же распределение видов в природе имеет вид промежуточной S -образной кривой 3 , что указывает на более сложный характер дифференциации и перекрывания ниш.

Распределение, изображаемое кривой 3 , называется логнормальным . Это связано с тем, что гистограмма распределения логарифмов log p i по октавам (диапазонам значений p i , отличающихся на границах в 2 раза) приближается по форме к нормальному распределению (рис. 1.8).

Значения n j (число точек, попавших в данную октаву j ) для различных октав с номерами j = …, –2, –1, 0, 1, 2,… (где 0 – октава с наибольшим числом точек) могут быть аппроксимированы выражением

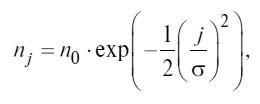
где σ – мера рассеяния относительно модального класса j = 0, которая для большинства анализируемых видовых группировок находится в пределах 1 ≤ σ ≤ 5.

Логнормальное распределение относительного доминирования характерно для сообществ с высокой видовой насыщенностью , в условиях, когда успех того или иного вида определяется большим числом относительно независимых и однородных по силе влияния факторов. В этом случае экологические ниши многомерны и перекрываются.

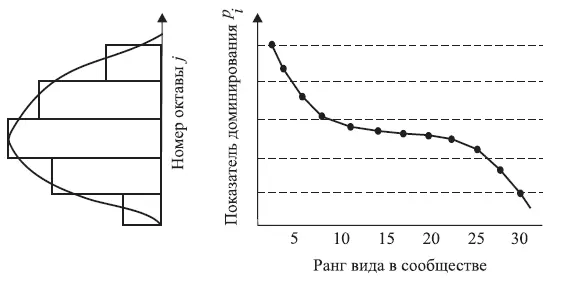
Рис. 1.8. Логнормальное распределение относительного доминирования видов

В общем случае расположения видов по степени значимости кривая доминирования не только точно отражает богатство и относительное обилие видов как компонентов видового разнообразия, но и объясняет, каким образом подразделяется пространство экологических ниш. Чем выше кривая и чем более она пологая, тем больше при данном числе видов общее их разнообразие. Чем круче идет кривая, тем меньше общее разнообразие и сильнее доминирование одного или нескольких видов. В стрессовых ситуациях независимо от того, вызваны ли они естественными причинами или антропогенным воздействием, кривая становится более крутой. Таким образом, кривую доминирования можно использовать для оценки влияния большинства нарушений среды существования на видовую структуру биоценоза.

Кроме видового богатства и типа рангового распределения для характеристики сообществ используется так называемый показатель разнообразия , который количественно отражает не только общее число видов, но и особенности количественного состава сообществ. К наиболее часто употребляемым относят:

• показатель разнообразия по Симпсону

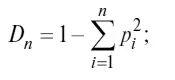
• показатель разнообразия по Шеннону

H = – Σ( p i / p )log 2( p i / p ),

где р i – численность (биомасса и т. п.) каждого i -го вида; р – общая численность (биомасса и т. п.) всех видов в сообществе;

• показатель выравненности Пиелу

E = H / H max,

где Н – реальное, а Н max– максимально возможное при данном числе видов значение коэффициента Шеннона. Последнее достигается при равенстве численности (биомассы и т. п.) всех видов в сообществе и рассчитывается согласно

H max = log 2 n .

Оба показателя разнообразия Симпсона и Шеннона обладают свойством принимать максимальное значение при равенстве долей всех видов в сообществе.

В случае, когда доля какого-нибудь одного вида, например i -го, стремится к 1, а всех остальных – к 0, оба показателя также стремятся к 0.

Из двух обобщенных индексов показатель Симпсона придает обычным видам больший вес, поскольку при возведении в квадрат малых значений p i получаются очень малые величины. Индекс Шеннона придает больший вес редким видам. Так как он заимствован из теории информации и представляет собой формализацию, которая широко используется при оценке сложности и содержания информации в любых типах систем и лучше всего подходит для целей сравнения в тех случаях, когда не интересуют компоненты разнообразия по отдельности.

При построении Одумом гистограммы для показателя разнообразия Симпсона для разных биоценозов выяснилось, что полученная гистограмма оказалась бимодальной: выделилась одна большая группа биоценозов с низким разнообразием (0,05–0,2) и другая большая группа со сравнительно высоким разнообразием (0,7–0,85). Во всей выборке не оказалось биоценоза с примерно равными значениями показателей относительного доминирования ( p 1= … = p n = 1/ n ), когда индекс разнообразия приближается к своему максимальному значению, т. е. к 1.