Коллектив авторов - Краткий курс по статистике
- Название:Краткий курс по статистике
- Автор:
- Жанр:
- Издательство:Литагент РИПОЛ
- Год:2015
- Город:Москва
- ISBN:978-5-409-00639-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Коллектив авторов - Краткий курс по статистике краткое содержание
Издание предназначено для студентов высших учебных заведений.
Краткий курс по статистике - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
☞ произведение каждого значения признака на соответствующую ему частоту равно произведению средней величины на сумму частот:
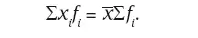
Средняя величина есть результат распределения объема совокупности поровну между всеми ее элементами;
☞ сумма квадратов отклонения индивидуальных значений признака от средней арифметической меньше суммы квадратов отклонения от любой другой величины:
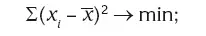
если увеличить или уменьшить все варианты осредняемого признака на какое-либо одно и то же число, то объем средней соответственно увеличится или уменьшится на это же число;
☞ если увеличить или уменьшить все варианты осредняемого признака в какое-либо число раз, то объем средней соответственно увеличится или уменьшится в это же количество раз;
☞ от увеличения или уменьшения веса каждого варианта признака в какое-либо число раз величина средней не изменится. Применение данного свойства удобно, если необходимо проанализировать совокупность со значительным количеством элементов, а частота элементов выражена многозначными числами. Если частоты элементов равны между собой, то среднюю можно рассчитать как невзвешенную;
☞ вследствие предыдущего свойства величина средней зависит не от абсолютных значений весов отдельных элементов, а от их доли в общей сумме весов, т. е. если не известны абсолютные выражения весов элементов, а известны пропорции между ними, то они могут использоваться для расчета средней;
☞ средняя арифметическая совокупности, состоящей из постоянных величин, равна этой постоянной:
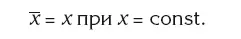
4. Приведем также формулы расчета средней гармонической, средней геометрической, средней квадратической и средней степенной величин.
Формула расчета степенной средней:
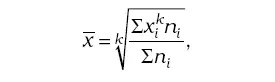
где x i – величины, для которых исчисляется средняя;
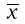 – средняя, где имеет место осреднение индивидуальных значений;
– средняя, где имеет место осреднение индивидуальных значений;
n – частота (повторяемость индивидуальных значений признака).
При к = формула превращается в формулу расчета средней гармонической.
Средняя гармоническая простая (невзвешенная) величина взаимосвязана со средней арифметической невзвешенной как величина, обратная средней арифметической, рассчитанная из обратных значений признака:
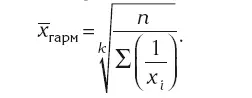
Средняя гармоническая взвешенная величина:
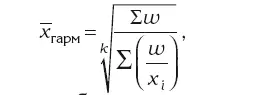
где ω – значения сводного, объемного, выступающего как признак-вес показателя.
Рассчитывается, когда имеются данные об объеме определяющего показателя, т. е. произведения осредняемого признака и признака-веса.
Также рассчитывается при наличии сведений об индивидуальных значениях осредняемого признака при отсутствии отдельных значений признака-веса.
Средняя степенная при показателе степени к = 0 становится средней геометрической величиной.
5. К основным видам средних геометрических величин относятся средняя геометрическая невзвешенная и средняя геометрическая взвешенная величины. Расчет средней геометрической невзвешенной величины: если показатель степени k = 0, то формула средней степенной
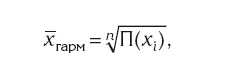
где П(х i ) – произведение индивидуальных значений осредняемого признака.
Применяется при наличии n коэффициентов роста. Индивидуальные значения признаков при этом становятся относительными величинами динамики (построены в виде цепных величин как отношение к предыдущему уровню каждого уровня в ряду динамики).
Средняя геометрическая невзвешенная величина характеризует средний коэффициент роста.
Средняя геометрическая взвешенная применяется в случае, если темпы роста остаются неизменными в течение нескольких периодов:
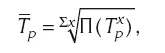
где 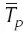 – средняя геометрическая взвешенная (средний темп прироста);
– средняя геометрическая взвешенная (средний темп прироста);
х – количество периодов, при которых темпы роста оставались неизменными.
6. Средняя квадратическая – средняя степенная при показателе степени k = 2.
Различают следующие основные виды средних квадратических величин: средняя квадратическая невзвешенная, средняя квадратическая взвешенная.
Средняя квадратическая невзвешенная
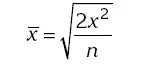
используется при расчете степени колеблемости индивидуальных значений признака вокруг средней арифметической. Средняя квадратическая взвешенная :
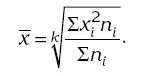
Все формы средней (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и т. д.) образованы от единой степенной средней и отличаются друг от друга показателями степени k.
Правильность расчета средней величины можно проверить с помощью правила мажорантности: чем выше степень рассчитываемой формы средней величины, тем больше значение средней:
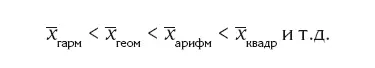
9. Медиана и мода. Абсолютные и относительные показатели вариации
1. Второй большой класс средних величин – структурные средние, используемые для определения структуры совокупности. К ним относятся мода и медиана. В отличие от степенных средних, рассчитывающихся на основе использования всех вариантов значений признака, медиана и мода характеризуют величину варианта, занимающего определенное среднее положение.
Для определения понятий моды и медианы требуется определение вариационного ряда. Построение ряда – процесс упорядочения количественного распределения элементов совокупности по значениям признака с последующим подсчетом числа элементов совокупности с этими значениями.
Читать дальшеИнтервал:
Закладка:










