Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

Трехфазные схемы переменного тока могут быть рассчитаны по той же методике, что и однофазные, если нагрузка в каждой фазе одинакова (симметричная нагрузка). Когда нагрузка несимметрична, решение становится более сложным. В этом примере приводится метод решения для случая несимметричной нагрузки (рис. 2.32).

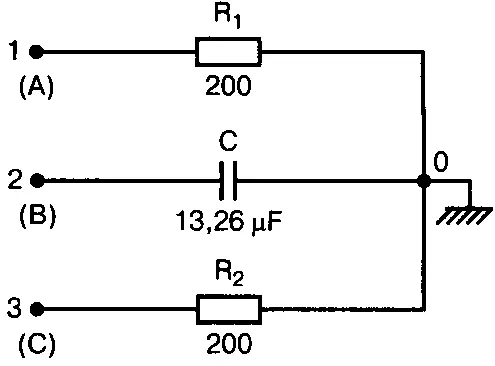
Рис. 2.32. Схема несимметричной трехфазной нагрузки

В этой задаче полные сопротивления ветвей нагрузки, включенной по схеме треугольника, равны: Z ab =25∠40° Ом; Z bc =10∠0° Ом и Z ca =20∠-60° Ом. Линейные напряжения равны 200 В при частоте 60 Гц. Фазовый угол для V ab равен 0°, и используется прямая последовательность фаз. Это означает, что V ab =200∠0° В, V bc =200∠-120° В и V ca =200∠120° В.

Начните решение с определения значений L и С . Они легко находятся вручную при известных значениях полных сопротивлений и частоты. Включите в ветви источников питания маленькие сопротивления, хотя в условии задачи они отсутствуют. Если этого не сделать, PSpice даст сообщение об ошибках, указывающее наличие петли напряжений. Сопротивления в линии включены, чтобы позволить вам находить линейные токи. На рис. 2.33 показана скорректированная схема. Входной файл для нее будет иметь вид:

Three Phase Unbalanced Load

VAB 12 2 AC 200V 0

VBC 20 0 AC 200V -120

VCA 10 1 AC 200V 120

RS1 12 1 0.01

RS2 20 2 0.01

RS3 10 0 0.01

RA 1 3 0.01

RB 2 4 0.01

RC 0 5 0.01

RAB 3 34 19.15

LAB 34 4 42.627mH

RBC 4 5 10

RCA 3 35 10

CCA 35 5 153.15uF

AC LIN 1 60Hz 60Hz

.print ac i(RA) iP(RA) iR(RA) ii(RA)

.print ac i(RB) iP(RB) iR(RB) ii(RB)

.print ac i(RC) iP(RC) iR(RC) ii(RC)

.opt nopage

.end

Рис. 2.33. Схема на рис. 2.32, скорректированная для проведения анализа на PSpice

Выполните анализ на PSpice и проверьте токи, показанные в выходном файле на рис. 2.34. Например, I(RA)=(16,09∠-5,136)=16,89 -17,7° А. Обратите внимание, что величина тока, обозначенная в выходном файле как I(RA), могла бы также быть определена как IM(RA). Покажите направления для каждого из токов на вашей схеме; без этого решение остается неопределенным. В качестве проверки добавьте линейные токи, чтобы видеть, что их сумма равна нулю. Учтите, что в результатах могут быть небольшие ошибки округления.

Three Phase Unbalanced Load

**** CIRCUIT DESCRIPTION

VAB 12 2 AC 200V 0

VBC 20 0 AC 200V - -120

VCA 10 1 AC 200V 120

RS1 12 1 0.01

RS2 20 2 0.01

RS3 10 0 0.01

RA 1 3 0.01

RB 2 4 0.01

RC 0 5 0.01

RAB 3 34 19.15

LAB 34 4 42.627mH

RBC 4 5 10

RCA 3 35 10

CCA 35 5 153.15uF

.AC LIN 1 60Hz 60Hz

.print ac i(RA) iP(RA) iR(RA) ii(RA)

.print ac i(RB) iP(RB) iR(RB) ii(RB)

.print ac i(RC) iP(RC) iR(RC) ii(RC)

. opt nopage

.end

**** AC ANALYSIS TEMPERATURE = 27.000 DEG С

FREQ I(RA) IP(RA) IR(RA) II(RA)

6.000E+01 1.639E+01 -1.770E+01 1.609E+01 -5.136E+00

FREQ I(RB) IP(RB) IR(RB) II(RB)

6.000E+01 2.016E+01 -1.430E+02 -1.609E+01 -1.215E+01

FREQ I(RC) IP(RC) IR(RC) II(RC)

6.000E+01 1.728E+01 9.001E+01 -3.292E-03 1.728E+01

Рис. 2.34. Выходной файл для схемы на рис. 2.33

Ток, потребляемый асинхронным двигателем, можно снизить, подключив к сети конденсатор. Проведем некоторые предварительные вычисления, рассматривая асинхронный двигатель в 5 лошадиных сил, который потребляет 53 А при 117 В при КПД 78,5 %. Входная мощность двигателя равна:

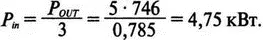
Полная мощность равна:

S = VI = 117·53 = 6,2 кВ·А.

По известным значениям Р и S можно найти реактивную мощность Q из треугольника мощностей:

S = P + JQ.

что дает для реактивной мощности

Q = 3,985 кВАР.

Сопротивление двигателя равно:

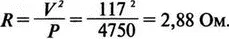
Реактивное сопротивление двигателя равно:

При частоте f =60 Гц это соответствует индуктивности

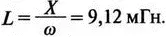
После решения задачи вручную может показаться, что здесь не требуется анализ на PSpice. Однако компьютерный анализ будет полезен, чтобы увидеть влияние подключения линейных конденсаторов. Обратимся к рис. 2.35, на котором показаны R и L для двигателя, наряду с двумя резистивными датчиками R A и R B. Их роли станут очевидными, когда мы добавим в схему конденсатор.

Рис. 2.35. Схема для анализа улучшения коэффициента мощности

Необходимо получить входной файл, который покажет общий ток и токи ветвей в зависимости от приложенного напряжения:

Single-Phase Motor, 5 hp

V 1 0 AC 117V

RA 1 2 0.01

RB 2 3 0.01

R 3 0 2.88

L 3 0 9.12mH

.AC LIN 1 60Hz 60Hz

.print ac i(RA) iP(RA) i(RB) iP(RB)

.print ac i(R) iP(R)

.print ac i(L) iP(L)

.opt nopage

.end

Выходной файл покажет следующие значения токов:

I(RA)=5.263Е+01, IP(RA)= -3.962Е+01

I(RB)=5.263E+01, IP(RB)= -3.962E+01

I(R) =4.034E+01, IP(R) = 3.310E-01

Значение линейного тока I(RA) близко к рассчитанному значению 53 А при фазовом угле, близком -40°. Коэффициент мощности pf (power factor) найден как косинус угла между векторами линейного тока и линейного напряжения:

pf = cos(-40°) = 0,76.

Сумма векторов токов ветвей (токи через R и L двигателя) равна линейному току. Теперь просто показать эффект подключения конденсатора между линиями (между узлами 2 и 0 ). Добавим во входной файл команду

С 2 0 380uF

и изменим одну из команд печати, чтобы включить в выходной файл ток через конденсатор. Теперь выполните анализ снова. Выходной файл покажет следующее:

I(RA) = 4.411Е+01, IP(RA) =-2.299Е+01

I(RB) = 5.296Е+01, IP(RB) = -3.993Е+01

I(C) = 1.676Е+01, IP(C) = 9.001Е+01

I(R) = 4.060E+01, IP(R) = 2.510E-02

I(L) = 3.401E+01, IP(L) = -8.997E+01

Мы видим, что линейный ток I(RA) уменьшился до 44,11 А при отстающем угле ≈23°, ясно показывая эффект повышения коэффициента мощности. Коэффициент мощности теперь равен

pf = cos(-23°) = 0,92.

Конденсатор проводит ток 16,76 А с фазовым углом 90°, вызывая изменение линейного тока. Обратите внимание, что ток через резистор датчика R B равен прежнему значению линейного тока, как и следовало ожидать.