Michel Anders - Написание скриптов для Blender 2.49

edgecount[edge.v1.index] = edgecount[edge.v1.index] + 1

Элемент словаря, на который мы ссылаемся с правой стороны выражения, не будет еще существовать всякий раз, когда мы ссылаемся на индекс вершины, с которой мы сталкиваемся впервые. Конечно, мы могли бы проверить это заранее, но это сделало бы код в целом гораздо менее читабельным.

from collections import defaultdict

def poleselect(me,n=5):

n_edges = defaultdict(int)

for e in me.edges:

n_edges[e.v1.index]+=1

n_edges[e.v2.index]+=1

for v in (v for v,c in n_edges.items() if c>=n ):

me.verts[v].sel=1

Хотя Блендер не является на самом деле программой САПР (CAD), множество людей используют его для САПР-подобных задач, как например, архитектурная визуализация. Блендер способен импортировать множество типов файлов, включая файлы основных САПР-программ, так что включение технических моделей, сделанных с точными размерами, никогда не было проблемой.

Эти САПР-программы часто предлагают все типы инструментальных средств для измерения размеров вашей модели (её частей), тогда как Блендер, по своей природе, обеспечивает лишь очень малую часть этих инструментов. Возможно узнать размер и позицию объекта, нажав клавишу N в окне 3D-вида. В режиме редактирования Вы можете включить отображение длин рёбер, углов между рёбрами, и площадей граней (смотри панель Mesh tools moreв контексте редактирования ( F9 ) окна Кнопок), но это почти всё, что можно выяснить.

Питон может преодолеть эти ограничения в ситуациях, когда нам нужны какие-либо специфические измерения, но мы не можем экспортировать нашу модель в САПР-программу. Практическим примером является вычисление объема меша. В настоящее время, множество компаний предлагают возможность восстановить вашу цифровую модель в виде объекта реального мира посредством методов 3D-печати. Я должен сказать, что это - особенное чувство, когда держишь пластиковую или даже металлическую копию вашей Блендер-модели в своих руках, это действительно добавляет целое новое измерение к 3D.

Сейчас основным компонентом цены 3D-печати модели является суммарный объём материала, который будет использован. Часто будет возможно разработать вашу модель как полый объект, который тратит меньше материала при производстве, но это очень неудобно - отправлять промежуточные версии вашей модели снова и снова, чтобы программное обеспечение изготовителя вычисляло объем и давало Вам ценовое предложение. Так что мы хотим иметь скрипт, который может вычислить объем меша достаточно точно.

Общий метод вычисления объема меша иногда именуется Формула Surveyor's(землемера), так как он связан со способом землемеров для вычисления объема холма или горы триангуляцией их поверхности.

Основная мысль в том, чтобы разбить триангулированный меш на множество колонн, которые имеют основание на плоскости xy.

Площадь поверхности треугольника проецируется на плоскость xy, умножается на среднюю координату z трех вершин - это даёт объем такой колонны. Суммирование по всем этим объемам даст в результате объем полного меша (смотри следующий рисунок).

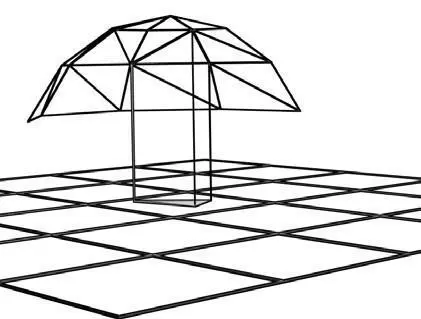
Есть пара вещей, которые должны быть приняты во внимание. Во-первых, меш может оказаться расширенным вниз от плоскости xy. Если мы создаем колонну от грани, которая лежит ниже плоскости xy, произведение спроецированной площади и средней координаты z будет отрицательным числом, так что мы должны вычесть эту величину, чтобы получить объем.

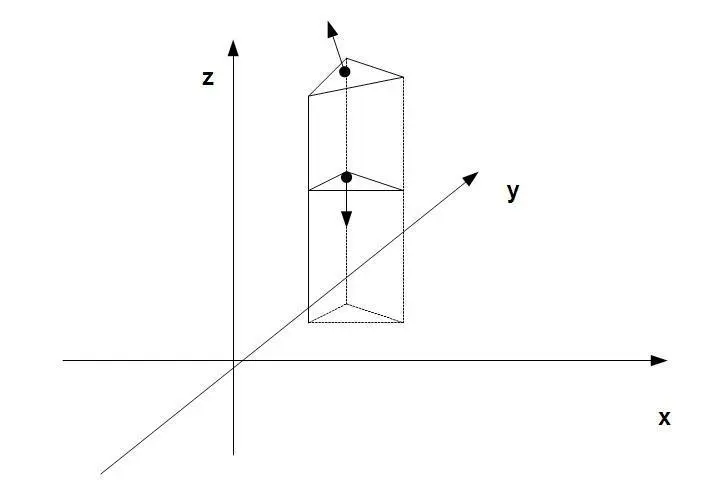
Во-вторых, меш может лежать полностью или частично выше плоскости xy. Если мы взглянем на пример на рисунке сверху, мы увидим что объект имеет два треугольника, которые дают вклад в объем объекта, верхний и нижний (вертикальные треугольники имеют нулевую спроецированную площадь, так что они не дают никакого вклада). Так как обе верхняя и нижняя грани лежат выше плоскости xy, мы должны вычесть объем колонны, создаваемой от нижней грани из объёма, созданного верхней гранью. Если объект будет полностью ниже плоскости xy, он будет с другой стороны, и мы должны будем вычесть объем верхней колонны из объема нижней колонны.

Мы можем сказать, что действие, которое нужно выполнить, определяется направлением нормалей наших треугольников. Если, например, треугольник - выше плоскости xy, но его нормаль указывает вниз (она имеет отрицательный z-компонент), тогда мы должны вычесть рассчитанный объем. Следовательно важно, чтобы все нормали единообразно указывали наружу (в режиме редактирования выберите все грани и нажмите Ctrl + N ).

Если мы принимаем во внимание все четыре возможности (нормаль грани направлена вверх или вниз, грань выше или ниже плоскости xy), мы можем написать следующую схему для нашей функции:

1. Убедиться, что у всех граней нормали единообразно указывают наружу.

2. Для всех граней

• Вычислить z-компоненту вектора нормали грани Nz

• Вычислить произведение P среднего числа z-координат и площади спроецированной поверхности.

• Если Nz положительно: прибавить P

• Если Nz отрицательно: вычесть P

Этот отличный алгоритм работает для простых объектов без отверстий так же, как и для объектов, содержащих отверстия (например, тор), или даже полых (то есть, содержащих объект, полностью заключенный в другом объекте), примеры приведены на следующем скриншоте:

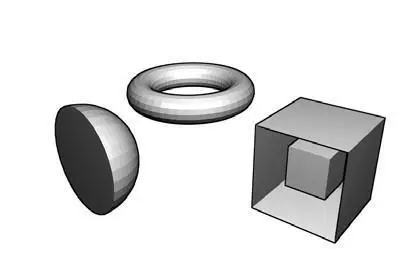
Поскольку мы допускаем, что произведение площади и координаты z может быть отрицательным, мы должны проверять только на направления нормали грани, чтобы охватить все ситуации.

Заметьте, что для меша необходимо быть закрытым и быть многогранником (manifold): Там не должно быть никаких отсутствующих граней, а также не должно быть никаких рёбер, которые не разделяют ровно двух граней, таких, как внутренние грани.

Важная часть кода показана здесь (полный скрипт называется volume.py):

def meshvolume(me):

volume = 0.0

for f in me.faces:

xy_area = Mathutils.TriangleArea(vec(f.v[0].co[:2]),

vec(f.v[1].co[:2]),vec(f.v[2].co[:2]))

Nz = f.no[2]

avg_z = sum([f.v[i].co[2] for i in range(3)])/3.0

partial_volume = avg_z * xy_area

if Nz < 0: volume -= partial_volume

if Nz > 0: volume += partial_volume

return volume

Выделенный код показывает, как мы вычисляем площадь треугольника, спроектированного на плоскость xy. TriangleArea() вычислит область двумерного треугольника, если ему передать двух-мерные точки (точки на плоскости xy). Итак, мы не передаем полные координатные векторов вершин, но усекаем их (то есть, мы отбрасываем координату z) до двух-компонентных векторов.