Виталий Леонтьев - Windows XP

«Слова», состоящие из восьми «букв», то есть восьмизначные двоичные числа, называются байтами. Восьмерка здесь присутствует не случайно: это первое мистическое компьютерное число. Откуда взялась в байте именно цифра 8, никто не знает (может быть, по количеству колонн Большого театра в Москве?). Но эта цифра постоянно буквально путается под ногами у компьютера. Позволю себе процитировать по этому поводу очень серьезную книгу американских специалистов, изданную ими в 1985 г.:

«Число битов, необходимых для кодирования символа в конкретной вычислительной машине, называется размером байта, а группа битов в этом числе называется байтом. Размер байта в большинстве ЭВМ равен 8» (выделение авторов).

То есть размер байта 8 бит устоялся в основном как оптимальный с точки зрения кодирования символов.

Примерами восьмизначных компьютерных «слов» - байтов можно записать следующие числа:

00001111 10101000 10001111 10000110 01010101 и так далее.

В каком же диапазоне изменяются наши 256 байтов? Очевидно, что от 0000 0000 до 1111 1111, при переводе в десятичную систему от 0 до 255.

Не путайте биты с байтами! Бит состоит из одной двоичной цифры, и разных битов всего два: 0 и 1. Байт содержит ровно восемь цифр, не больше и не меньше. А сколько всего имеется разных байтов? Это легко выяснить из предыдущей таблицы: 256.

Получили второе мистическое компьютерное число - 256. Компьютер все время работает с байтами, обычно ими легче оперировать. Но по мере развития прогресса компьютеры становились все мощнее и мощнее, все мозговитее и мозговитее. Байтов в них становилось все больше и больше. Сейчас их уже так много, что разработана целая система так называемых производных единиц от байта.

Короче, сначала придумали третье компьютерное число, равное 2 = 1024. Почему такое? Очень просто. Во-первых, круглая степень - 10. Во-вторых, 1024 почему-то почти равно 1000. А 1000 - это основание для обычных производных единиц: 1 километр равен 1000 метров, 1 килограмм равен 1000 граммов. Дело даже дошло до того, что один немецкий компьютерный журнал поместил изображение 1 киломарки, равной 1024 маркам…

Затем постановили, что 1024 байта равны 1 - правильно! - килобайту.А 1024 килобайта равны 1 мегабайту,и так далее. Все имеющиеся производные единицы байта находятся в следующей таблице.

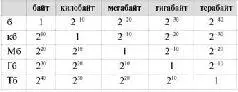
Только будьте внимательны при использовании производных единиц! Полностью их имена пишутся с маленькой буквы, а сокращенно - с большой (но байт сокращается до маленькой буквы).

¦ 1 килобайт = 1 кб = 1 К = 210 б;

¦ 1 мегабайт = 1 Мб = 1 М = 210 К = 220 б;

¦ 1 гигабайт = 1 Гб = 1 Г = 210 М = 220 К = 230 б.

Как же перевести число из привычной нам десятичной системы в двоичную?

Проще всего - с помощью инженерного калькулятора. Если же такового под рукой не окажется, можно произвести это преобразование с помощью обычной бумаги и карандаша. Наиболее известный и простой способ перевода из десятичной системы в двоичную производится в десятичной системе путем деления на 2 - на основание двоичной системы. Приведем алгоритм перевода чисел из десятичной системы в двоичную, состоящий из двух шагов.

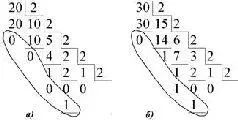
Число в десятичной системе делится на 2. Получаем частное и остаток. Частное снова делится на 2. Снова получаем частное и остаток. Опять делим новое частное на 2 и так далее. Остатки от деления - цифры 0 и 1 - являются цифрами соответствующего двоичного числа, записанными справа налево.

Процесс деления прекращается, когда частное становится равным нулю. В первом случае (а) у нас 20 10 = 10100 2 . Во втором случае (б) получается 30 10 = 11110 2 .

А наоборот?

Наиболее прост такой способ превращения двоичного числа в десятичное. Подпишем под последней цифрой двоичного числа десятичное число 2° = 1, под второй цифрой справа - число 2 1 = 2, следующей цифрой - число 2 2 = 4, под четвертой - число 2 3 = 8 и так далее. Затем просто сложим те десятичные числа - степени двойки - над которыми стоят двоичные цифры 1.

Например:

10101000 2 = 128 10 + 32 10 + 8 10 = 168 10 .

010101012 = 6410 + 1610 + 410 + 110= 8510.

Кроме двоичной системы счисления, в компьютерной практике также используется шестнадцатеричная система. На практике она используется даже чаще, чем двоичная: при задании цветов страницы сайта, при доступе к символам современных двухбайтовых шрифтов, при программировании, особенно на ассемблере… Дело в том, что байт кодируется в точности двузначным шестнадцатеричным числом, что гораздо более просто и читабельно, чем в двоичной системе. Но об этом ниже.

В некотором смысле шестнадцатеричная система еще хуже, чем двоичная. Судите сами. Сколько цифр в шестнадцатеричной системе? Ровно 16. И какими же цифрами их обозначать? А вот какими:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F.

Здесь ровно 16 цифр. Последние шесть цифр взяты из латинского алфавита и читаются так:

¦ А - цифра «а». Это цифра «десять»;

¦ В - цифра «бэ» - цифра «одиннадцать»;

¦ С - цифра «цэ» - «двенадцать»;

¦ D - цифра «дэ» - «тринадцать»;

¦ Е - цифра «е» - «четырнадцать»;

¦ F - цифра «эф» - «пятнадцать».

Как видите, проблемы с русским языком стали еще серьезней. Первые шестнадцатеричные числа мы выписывать не будем, а укажем только ключевые моменты получения следующего шестнадцатеричного числа, которых, в отличие от двоичной системы, не один, а уже четыре.

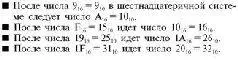
Лучше понять шестнадцатеричную систему можно, изучая ее таблицу сложения:

Из шестнадцатеричной системы в десятичную числа переводятся так же, как и из двоичной, только, конечно, нужно делить не на 2, а на 16, а остатки, значения которых будут от О до 15, переводить в шестнадцатеричные цифры. Обратный перевод осуществляется так же, как было представлено десятичное число в начале главы, только в степень возводится число 16. Например:

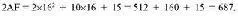
Гораздо интереснее переводить двоичные числа в шестнадцатеричные и обратно.