Владимир Большаков - КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия

Укажите одну вершину в нижней грани и две в верхней. В Дереве модели появится объект Плоскость через три вершины: 3.

Выполните команды Операции | Сечение | Поверхностью. В Дереве модели укажите объект Плоскость через три вершины: 3.

В Панели свойств укажите направление отсечения: Обратное направление. Нажмите кнопку Создать объект:

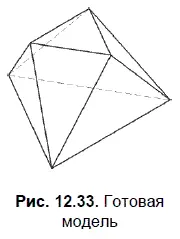
Результат приведен на рис. 12.33.

Условие. Создать твердотельную модель призматоида с гранями — трапециями (см. рис. 12.3, б ).

Решение. В этом примере сопоставим применение пользовательских ориентаций Изометрия XYZи Изометрия YZX. Далее описаны действия, необходимые для создания 3D-модели призматоида.

1. Выполните команду Файл | Создать | Деталь.

На панели Виднажмите кнопку списка справа от кнопки Ориентация:

Укажите вариант Изометрия XYZ.

В Дереве модели укажите Плоскость ZX. Введите название модели — Призматоид_2.

Нажмите кнопку Эскизна панели Текущее состояние:

2. В появившейся Компактной панелинажмите кнопку переключения Геометриядля вызова соответствующей Инструментальной панели:

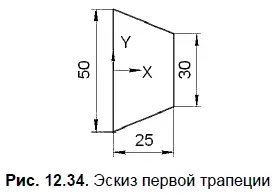
3. На панели Глобальные привязкивключите привязку По сеткеи изображение сетки на экране. Изобразите трапецию (рис. 12.34), выбрав команду Непрерывный ввод объектов:

4. Нажмите кнопку Операция выдавливания:

на панели Редактирование детали:

Внизу экрана появится Панель свойств, на которой установите параметры выдавливания: Прямое направление; Расстояние 1 — 30.0; Угол внутрь; Угол 1 — 15. Ввод параметров заканчивается нажатием кнопки Создать объект:

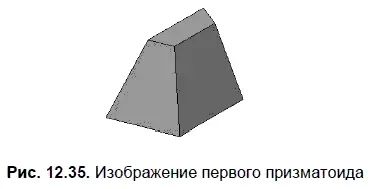
После включения Ориентация | Изометрия XYZи команды Полутоновоена панели Видполучится показанное на рис. 12.35 изображение призматоида.

5. Выполните команды Файл | Создать | Деталь.

Выберите Вид | Ориентация | Изометрия YZX.

В Дереве модели укажите Плоскость XY. Введите название модели — Призматоид_3. Откройте эскиз и изобразите трапецию по указанным размерам (рис. 12.36).

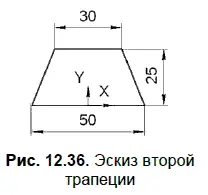
6. Закройте эскиз. Нажмите кнопку Операция выдавливания:

на панели Редактирование детали:

Внизу экрана появится Панель свойств, на которой установите параметры выдавливания: Прямое направление; Расстояние 1 — 30.0; Угол внутрь; Угол 1 — 15. Ввод параметров заканчивается нажатием кнопки Создать объект:

После включения Ориентация | Диметрияи команды Полутоновоена панели Видполучится показанное на рис. 12.37 изображение призматоида.

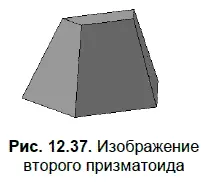
Итак, видно, что одинаково расположенные 3D-модели, созданные с применением разных пользовательских ориентаций, получаются по эскизам, расположенным по-разному. При этом связь между расположением эскизов и моделей далеко не очевидна. Преимуществом применения пользовательской ориентации Изометрия XYZявляется получение по 3D-модели адекватно расположенных ортогональных проекций моделируемых объектов.

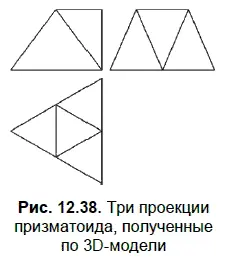
На рис. 12.38 показаны три проекции призматоида с треугольными гранями, полученные в результате выполнения команд Файл | Создать | Чертеж | Вставка | Вид с модели | Стандартные.

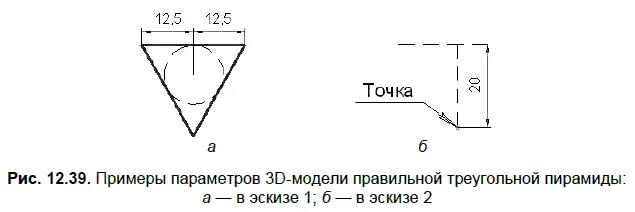
Если 3D-модель тетраэдра можно построить по одному параметру, например по длине ребра, то для создания модели правильной треугольной пирамиды требуются два параметра. В наиболее очевидном способе создания 3D-модели первый параметр определяет геометрию основания (равностороннего треугольника), второй параметр задает высоту пирамиды. При использовании пользовательской ориентации Изометрия XYZи операции По сечениямдля создания правильной треугольной пирамиды эскиз 1 в плоскости zx может иметь вид, показанный на рис. 12.39, а, а эскиз 2 (одна точка) в плоскости zy — вид, показанный на рис. 12.39, б.

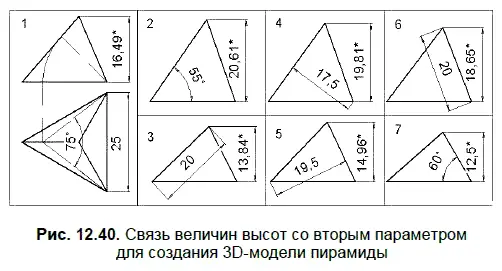
На рис. 12.40 представлены еще 7 способов создания 3D-модели правильной треугольной пирамиды, когда первый параметр — длина ребра основания, равная 25 мм, а вторым параметром является следующая величина:

1. Угол между боковыми гранями (75).

2. Угол между основанием и боковым ребром (55°).

3. Длина бокового ребра (20 мм).

4. Расстояние между скрещивающимися ребрами (17,5 мм).

5. Расстояние между боковой гранью и противолежащей вершиной (19,5 мм).

6. Высота боковой грани (20 мм).

7. Угол между основанием и боковой гранью (60°).

На рис. 12.40 со знаком «*» указан также зависимый параметр — высота пирамиды, построенной по двум заданным параметрам.

Величины высот, показанные на рис. 12.39, могут быть найдены в результате решения элементарных планиметрических задач, или в результате несложных построений с последующим измерением искомой величины.

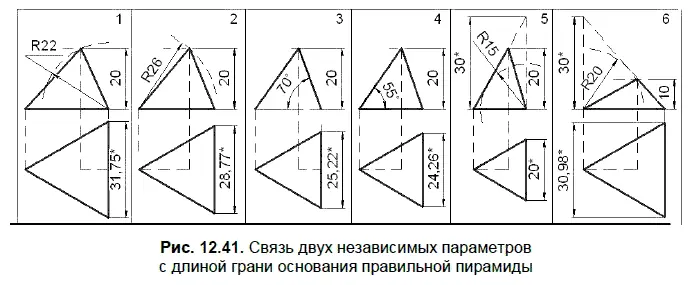
На рис. 12.41 представлены 6 способов создания 3D-модели правильной треугольной пирамиды, когда первый параметр задает высоту пирамиды (например, равную 20 мм), а вторым параметром является следующая величина: