Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

Для операций, составляющих линейный участок программы, могут применяться следующие виды оптимизирующих преобразований:

• удаление бесполезных присваиваний;

• исключение избыточных вычислений (лишних операций);

• свертка операций объектного кода;

• перестановка операций;

• арифметические преобразования.

Далее рассмотрены два метода оптимизации линейных участков: исключение лишних операций и свертка объектного кода.

Свертка объектного кода – это выполнение во время компиляции тех операций исходной программы, для которых значения операндов уже известны. Нет необходимости многократно выполнять эти операции в результирующей программе – вполне достаточно один раз выполнить их при компиляции.

Внимание!

Не следует путать оптимизацию по методу свертки объектного кода с рассмотренным в лабораторной работе № 3 алгоритмом «сдвиг-свертка». Свертка объектного кода и свертка по правилам грамматики при выполнении синтаксического разбора– это принципиально разные операции!

Простейший вариант свертки – выполнение в компиляторе операций, операндами которых являются константы. Несколько более сложен процесс определения тех операций, значения которых могут быть известны в результате выполнения других операций. Для этой цели при оптимизации линейных участков программы используется специальный алгоритм свертки объектного кода.

Алгоритм свертки для линейного участка программы работает со специальной таблицей Т, которая содержит пары (<���переменная>,<���константа>) для всех переменных, значения которых уже известны. Кроме того, алгоритм свертки помечает те операции во внутреннем представлении программы, для которых в результате свертки уже не требуется генерация кода. Так как при выполнении алгоритма свертки учитывается взаимосвязь операций, то удобной формой представления для него являются триады, поскольку в других формах представления операций (таких как тетрады или команды ассемблера) требуются дополнительные структуры, чтобы отразить связь результатов одних операций с операндами других.

Рассмотрим выполнение алгоритма свертки объектного кода для триад. Для пометки операций, не требующих порождения объектного кода, будем использовать триады специального вида С(К,0).

Алгоритм свертки триад последовательно просматривает триады линейного участка и для каждой триады делает следующее:

1. Если операнд есть переменная, которая содержится в таблице Т, то операнд заменяется на соответствующее значение константы.

2. Если операнд есть ссылка на особую триаду типа С(К,0), то операнд заменяется на значение константы К.

3. Если все операнды триады являются константами, то триада может быть свернута. Тогда данная триада выполняется и вместо нее помещается особая триада вида С(К,0), где К – константа, являющаяся результатом выполнения свернутой триады. (При генерации кода для особой триады объектный код не порождается, а потому она в дальнейшем может быть просто исключена.)

4. Если триада является присваиванием типа А:=В, тогда:

• если В – константа, то А со значением константы заносится в таблицу Т (если там уже было старое значение для А, то это старое значение исключается);

• если В – не константа, то А вообще исключается из таблицы Т, если оно там есть.

Рассмотрим пример выполнения алгоритма.

Пусть фрагмент исходной программы (записанной на языке типа Pascal) имеет вид:

I:= 1 + 1;

I:= 3;

J:= 6*I + I;

Ее внутреннее представление в форме триад будет иметь вид:

1: + (1,1)

2::= (I, ^1)

3::= (I, 3)

4: * (6, I)

5: + (^4, I)

6::= (J, ^5)

Процесс выполнения алгоритма свертки показан в табл. 4.1.

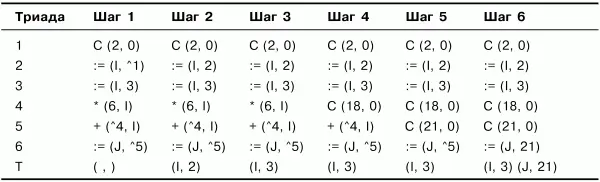
Если исключить особые триады типа C(K,0) (которые не порождают объектного кода), то в результате выполнения свертки получим следующую последовательность триад:

1::= (I, 2)

2::= (I, 3)

3::= (J, 21)

Видно, что результирующая последовательность триад может быть подвергнута дальнейшей оптимизации – в ней присутствуют лишние присваивания, но другие методы оптимизации выходят за рамки данной лабораторной работы (с ними можно познакомиться в [1, 2, 7]).

Алгоритм свертки объектного кода позволяет исключить из линейного участка программы операции, для которых на этапе компиляции уже известен результат. За счет этого сокращается время выполнения, [7]а также объем кода результирующей программы.

Свертка объектного кода, в принципе, может выполняться не только для линейных участков программы. Когда операндами являются константы, логика выполнения программы значения не имеет – свертка может быть выполнена в любом случае. Если же необходимо учитывать известные значения переменных, то нужно принимать во внимание и логику выполнения результирующей программы. Поэтому для нелинейных участков программы (ветвлений и циклов) алгоритм будет более сложным, чем последовательный просмотр линейного списка триад.

Исключение избыточных вычислений (лишних операций) заключается в нахождении и удалении из объектного кода операций, которые повторно обрабатывают одни и те же операнды.

Операция линейного участка с порядковым номером i считается лишней операцией, если существует идентичная ей операция с порядковым номером j, j< i и никакой операнд, обрабатываемый операцией с порядковым номером i, не изменялся никакой другой операцией, имеющей порядковый номер между i и j.

Алгоритм исключения лишних операций просматривает операции в порядке их следования. Так же как и алгоритму свертки, алгоритму исключения лишних операций проще всего работать с триадами, потому что они полностью отражают взаимосвязь операций.

Рассмотрим алгоритм исключения лишних операций для триад.

Чтобы следить за внутренней зависимостью переменных и триад, алгоритм присваивает им некоторые значения, называемые числами зависимости, по следующим правилам:

• изначально для каждой переменной ее число зависимости равно 0, так как в начале работы программы значение переменной не зависит ни от какой триады;

• после обработки i-й триады, в которой переменной А присваивается некоторое значение, число зависимости A (dep(A)) получает значение i, так как значение А теперь зависит от данной i-й триады;

• при обработке i-й триады ее число зависимости (dep(i)) принимается равным значению 1+ (максимальное_из_чисел_зависимости_операндов).

Таким образом, при использовании чисел зависимости триад и переменных можно утверждать, что если i – я триада идентична j-й триаде (j