Миран Липовача - Изучай Haskell во имя добра!

ghci> map (\(a,b) –> a + b) [(1,2),(3,5),(6,3),(2,6),(2,5)]

[3,8,9,8,7]

Обычно анонимные функции заключаются в круглые скобки, если только мы не хотим, чтобы лямбда-выражение заняло всю строку. Интересная деталь: поскольку все функции каррированы по умолчанию, допустимы две эквивалентные записи.

addThree :: Int -> Int -> Int -> Int

addThree x y z = x + y + z

addThree' :: Int -> Int -> Int -> Int

addThree' = \x -> \y -> \z -> x + y + z

Если мы объявим функцию подобным образом, то станет понятно, почему декларация типа функции представлена именно в таком виде. И в декларации типа, и в теле функции имеются три символа –>. Конечно же, первый способ объявления функций значительно легче читается; второй – это всего лишь очередная возможность продемонстрировать каррирование.

ПРИМЕЧАНИЕ.Обратите внимание на то, что во втором примере анонимные функции не заключены в скобки. Когда вы пишете анонимную функцию без скобок, предполагается, что вся часть после символов –>относится к этой функции. Так что пропуск скобок экономит на записи. Конечно, ничто не мешает использовать скобки, если это вам больше нравится.

Тем не менее есть случаи, когда использование такой нотации оправдано. Я думаю, что функция flipбудет лучше читаться, если мы объявим её так:

flip' :: (a –> b –> c) –> b –> a –> c

flip' f = \x y –> f y x

Несмотря на то что эта запись равнозначна flip' f x y = f y x, мы даём понять, что данная функция чаще всего используется для создания новых функций. Самый распространённый сценарий использования flip– вызов её с некоторой функцией и передача результирующей функции в mapили zipWith:

ghci> zipWith (flip (++)) ["люблю тебя", "любишь меня"] ["я ", "ты "]

["я люблю тебя","ты любишь меня"]

ghci> map (flip subtract 20) [1,2,3,4]

[19,18,17,16]

Итак, используйте лямбда-выражения таким образом, когда хотите явно показать, что ваша функция должна быть частично применена и передана далее как параметр.

Когда мы разбирались с рекурсией, то во всех функциях для работы со списками наблюдали одну и ту же картину. Базовым случаем, как правило, был пустой список. Мы пользовались образцом (x:xs)и затем делали что-либо с «головой» и «хвостом» списка. Как выясняется, это очень распространённый шаблон. Были придуманы несколько полезных функций для его инкапсуляции. Такие функции называются свёртками (folds). Свёртки позволяют свести структуру данных (например, список) к одному значению.

Функция свёртки принимает бинарную функцию, начальное значение (мне нравится называть его «аккумулятором») и список. Бинарная функция принимает два параметра. Она вызывается с аккумулятором и первым (или последним) элементом из списка и вычисляет новое значение аккумулятора. Затем функция вызывается снова, с новым значением аккумулятора и следующим элементом из списка, и т. д. То, что остаётся в качестве значения аккумулятора после прохода по всему списку, и есть результат свёртки.

Для начала рассмотрим функцию foldl– свёртка слева. Она сворачивает список, начиная с левой стороны. Бинарная функция применяется для начального значения и первого элемента списка, затем для вновь вычисленного аккумулятора и второго элемента списка и т. д.

Снова реализуем функцию sum, но на этот раз будем пользоваться свёрткой вместо явной рекурсии.

sum' :: (Num a) => [a] –> a

sum' xs = foldl (\acc x –> acc + x) 0 xs

Проверка – раз, два, три!

ghci> sum' [3,5,2,1]

11

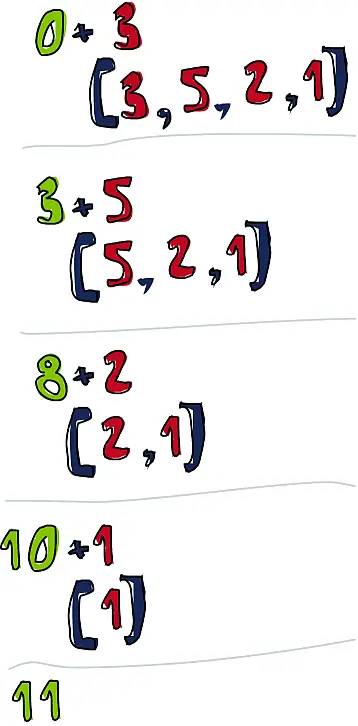
Давайте посмотрим более внимательно, как работает функция foldl. Бинарная функция – это лямбда-выражение (\acc x –> acc + x), нуль – стартовое значение, и xs– список. В самом начале нуль используется как значение аккумулятора, а 3– как значение образца x(текущий элемент). Выражение (0+3)в результате даёт 3; это становится новым значением аккумулятора. Далее, 3используется как значение аккумулятора и 5– как текущий элемент; новым значением аккумулятора становится 8. На следующем шаге 8– значение аккумулятора, 2– текущий элемент, новое значение аккумулятора становится равным 10. На последнем шаге 10из аккумулятора и 1как текущий элемент дают 11. Поздравляю – вы только что выполнили свёртку списка!

Диаграмма на предыдущей странице иллюстрирует работу свёртки шаг за шагом, день за днём. Цифры слева от знака + представляют собой значения аккумулятора. Как вы можете видеть, аккумулятор будто бы «поедает» список, начиная с левой стороны. Ням-ням-ням! Если мы примем во внимание, что функции каррированы, то можем записать определение функции ещё более лаконично:

sum' :: (Num a) => [a] –> a

sum' = foldl (+) 0

Анонимная функция (\acc x –> acc + x)– это то же самое, что и оператор (+). Мы можем пропустить xsв параметрах, потому что вызов foldl (+) 0вернёт функцию, которая принимает список. В общем, если у вас есть функция вида foo a = bar b a, вы всегда можете переписать её как foo = bar b, так как происходит каррирование.

Ну что ж, давайте реализуем ещё одну функцию с левой свёрткой перед тем, как перейти к правой. Уверен, все вы знаете, что функция elemпроверяет, является ли некоторое значение частью списка, так что я не буду этого повторять (тьфу ты – не хотел, а повторил!). Итак:

elem' :: (Eq a) => a –> [a] –> Bool

elem' y ys = foldl (\acc x –> if x == y then True else acc) False ys

Что мы имеем? Стартовое значение и аккумулятор – булевские значения. Тип аккумулятора и стартового значения в свёртках всегда совпадают. Запомните это правило: оно может подсказать вам, что следует использовать в качестве стартового значения, если вы затрудняетесь. В данном случае мы начинаем со значения False. В этом есть смысл: предполагается, что в списке нет искомого элемента. Если мы вызовем функцию свёртки с пустым списком, то результатом будет стартовое значение. Затем мы проверяем текущий элемент на равенство искомому. Если это он – устанавливаем в True. Если нет – не изменяем аккумулятор. Если он прежде был равен значению False, то остаётся равным False, так как текущий элемент – не искомый. Если же был равен True, мы опять-таки оставляем его неизменным.

Правая свёртка, foldr, работает аналогично левой, только аккумулятор поглощает значения, начиная справа. Бинарная функция левой свёртки принимает аккумулятор как первый параметр, а текущее значение – как второй (\acc x –>… ); бинарная функция правой свёртки принимает текущее значение как первый параметр и аккумулятор – как второй (\x acc –>… ). То, что аккумулятор находится с правой стороны, в некотором смысле логично, поскольку он поглощает значения из списка справа.