У Клоксин - ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

найтивce(X,G,_):-asserta(найденo(мapкep)), call(G), asserta(найденo(X)),fail.

найтивсе(_,_,L):- собрать_найденное([],М),!, L=M.

собрать_найденное(S,L):- взятьеще(Х),!,собрать_найденное([Х |S],L).

собрать_найденное(L,L).

взятьеще(Х):- retract(найдено(Х)),!, Х\==маркер.

Предикат найтивсе,начинает свою работу с занесения специального маркера, который представляет из себя структуру с функтором найденои с компонентой маркер.Этот специальный маркер отмечает место в базе данных, перед которым будут занесены (с помощью asserta)все X,согласующие Gс базой данных при данном запуске найтивсе.Затем делается попытка согласовать Gи каждый раз, когда это удается, Xзаносится в базу данных в качестве компоненты функтора найдено.Предикат failинициирует процесс возврата и попытку повторно согласовать G (assertaсогласуется не более одного раза). Когда попытка согласовать Gзавершается неудачей, процесс возврата приводит к неудаче первого утверждения из определения найтивсе,и делается попытка согласовать в качестве цели второе утверждение. Второе утверждение вызывает собрать_найденноедля выборки из базы данных всех структур найдено и включения их компонент в список. Предикат собрать_найденноевставляет каждый элемент в переменную, где хранится список «уже собранных» элементов. Этот прием мы рассматривали выше при разборе программы ге-натом. Как только встречается компонента маркер, взятьещезавершается неудачей, после чего выбирается второе утверждение для собрать_найденное.При сопоставлении его с текущей целью второй аргумент (результат) сцепляется с первым аргументом (с набранным списком)

Заметим, что присутствие в базе данных структуры найдено (маркер)указывает на некоторое конкретное употребление найтивсе. Это означает, что найтивсеможет вызываться рекурсивно – любое использование найтивсево втором аргументе другого найтивсебудет обработано правильно.

В разд. 7.9 мы разработаем программу, которая использует предикат найтивседля построения списка всех потомков узла в графе. Этот список необходим для реализации программы поиска по графу вширь.

Упражнение 7.7.Напишите Пролог-программу случайный_выбортакую, что цель случайный_выбор(L, Е)конкретизирует Е случайно выбранным элементом списка L. Подсказка: используйте генератор случайных чисел и определите предикат, который возвращает N-й элемент списка.

Упражнение 7.8.Задана цель найтивсе(Х,G, L). Что произойдет, если в Gимеются неконкретизированные переменные не сцепленные с X?

Граф – это сеть, состоящая из узлов, соединенных дугами. Например, географическую карту можно рассматривать как граф, где узлами являются населенные пункты, а дугами, соединяющие их дороги. Если вы хотите найти кратчайший маршрут между двумя населенными пунктами, вам предстоит решить задачу нахождения кратчайшего пути между двумя узлами графа.

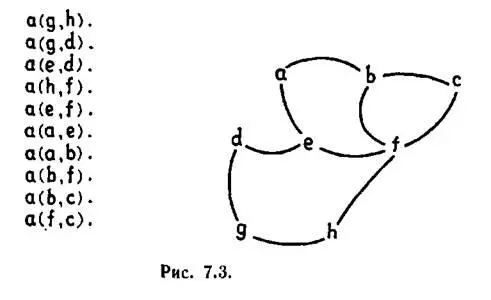
Проще всего описать граф в базе данных с помощью фактов, представляющих дуги между узлами графа. На рис, 7.3 приведен пример графа и его представления с помощью фактов. Чтобы пройти от узла gк узлу а, мы можем пойти по пути g, d, e, аили по одному из многих других возможных путей. Если мы представляем ориентированный граф, то предикат а следует понимать так, что а(Х, Y)означает, что существует дуга из Xв Y, но из этого не следует существование дуги из Yв X. В данном разделе мы будем иметь дело только с неориентированными графами, у которых все дуги двунаправленные. Это допущение совпадает с тем, которое мы делаем в разд. 7.2 при поиске в лабиринте.

Простейшая программа поиска по графу, представленному так, как указано выше, выглядит следующим образом:

переход(Х,X).

переход(Х,Y):- (a(X,Z);a(Z,X)), переход(Z,Y).

К сожалению, эта программа может зацикливаться. Поэтому, как и раньше, мы используем список Т для хранения перечня тех узлов, в которых мы уже побывали в какой-либо рекурсии предиката.

переход(Х,Х,Т).

переход(Х,Y,T):- (a(X,Z);a(Z,X)), not (принадлежит(Z, Т)),переход(Z, Y,[Z|T]).

Эта программа, разработанная в разд. 7.2, осуществляет так называемый поиск «вглубь», поскольку вначале рассматривается только один из соседей узла по графу, Другие же соседи игнорируются до тех пор, пока неудачные попытки согласовать цели в рекурсивных вызовах не возвратят Пролог к рассмотрению данного узла.

Теперь давайте рассмотрим такой поиск по графу, который мог бы быть полезен на практике. Как быть, если мы должны спланировать маршрут поездки из одного города Северной Англии в другой? Для этого потребуется база данных с информацией о дорогах между городами в Северной Англии и их протяженности:

а(ньюкасл,карлайл,58).

а(карлайл,пенрит,23).

а(дарлингтон,ньюкасл,40).

а(пенрит, дарлингтон,52).

а(уэркингтон,карлайл,33).

а(уэркингтон,пенрит,39).

На некоторое время мы можем забыть о расстояниях и определить новый предикат:

a(X,Y):- a(X,Y,Z).

С помощью этого определения предиката а уже имеющаяся программа поиска по графу ( переход) будет находить пути, по которым можно переезжать из одного места на графе в любое другое. Однако программа переходимеет недостаток: когда она успешно завершается, мы не знаем, какой путь она нашла. По меньшей мере мы вправе ожидать от программы переход выдачинам в нужном порядке списка мест, которые придется посетить. Тем более, что в программе имеется перечень этих мест, правда, в порядке, обратном тому, какой нам нужен. Чтобы получить правильный список, мы можем воспользоваться программой обр, определенной в разд. 7.5. Тогда мы получим новое определение программы переход, которая возвращает найденный маршрут через свой третий аргумент:

переход(Старт,Цель,Путь):- переход0(Старт,Цель,[],R),обр(R, Путь).

переход0(Х,Х,Т,[Х|Т]).

переход0(Место,Y,Т,R):-следузел(Место,Т,Сосед),переход0(Сосед,Y,[Место|T],R).

следузел(Х,Бывали,Y):- (a(X,Y); a(Y,X)),not (принадлежит(Y,Бывали)).

Заметим, что предикат следузелпозволяет получать для узла X«правильный» узел Y, т. е. такой, к которому можно непосредственно перейти от узла X. Ниже приводится пример работы этой программы при поиске маршрута из Дарлингтона в Уэркингтон: