Иван Братко - Программирование на языке Пролог для искусственного интеллекта

• разбить L на два списка L1 и L2 примерно одинаковой длины;

• произвести сортировку списков L1 и L2,получив списки S1 и S2;

• слить списки S1 и S2, завершив на этом сортировку списка L.

Реализуйте этот принцип сортировки и сравните его эффективность с эффективностью программы быстрсорт.

Списки часто применяют для представления множеств. Такое использование списков имеет тот недостаток, что проверка принадлежности элемента множеству оказывается довольно неэффективной. Обычно предикат принадлежит( X, L)для проверки принадлежности X к L программируют так:

принадлежит X, [X | L] ).

принадлежит X, [ Y | L] ) :-

принадлежит( X, L).

Для того, чтобы найти X в списке L, эта процедура последовательно просматривает список элемент за элементом, пока ей не встретится либо элемент X, либо конец списка. Для длинных списков такой способ крайне неэффективен.

Для облегчения более эффективной реализация отношения принадлежности применяют различные древовидные структуры. В настоящем разделе мы рассмотрим двоичные деревья.

Двоичное дерево либо пусто, либо состоит из следующих трех частей:

• корень

• левое поддерево

правое поддерево

Корень может быть чем угодно, а поддеревья должны сами быть двоичными деревьями. На рис. 9.4 показано представление множества [а, b, с, d] двоичным деревом. Элементы множества хранятся в виде вершин дерева. Пустые поддеревья на рис. 9.4 не показаны. Например, вершина b имеет два поддерева, которые оба пусты.

Существует много способов представления двоичных деревьев на Прологе. Одна из простых возможностей — сделать корень главным функтором соответствующего терма, а поддеревья — его аргументами. Тогда дерево рис. 9.4 примет вид

а( b, с( d) )

Такое представление имеет среди прочих своих недостатков то слабое место, что для каждой вершины дерева нужен свой функтор. Это может привести к неприятностям, если вершины сами являются структурными объектами.

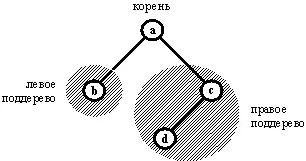
Рис. 9.4. Двоичное дерево.

Существует более эффективный и более привычный способ представления двоичных деревьев: нам нужен специальный символ для обозначения пустого дерева и функтор для построения непустого дерева из трех компонент (корня и двух поддеревьев). Относительно функтора и специального символа сделаем следующий выбор:

• Пусть атом nilпредставляет пустое дерево.

• В качестве функтора примем дер, так что дерево с корнем X, левым поддеревом Lи правым поддеревом Rбудет иметь вид терма дер( L, X, R)(см. рис. 9.5).

В этом представлении дерево рис. 9.4 выглядит как

дер( дер( nil, b, nil), a,

дер( дер( nil, d, nil), с, nil) ).

Теперь рассмотрим отношение принадлежности, которое будем обозначать внутри. Цель

внутри( X, T)

истинна, если Xесть вершина дерева T. Отношение внутриможно определить при помощи следующих правил:

X есть вершина дерева T, если

• корень дерева T совпадает с X, или

• X — это вершина из левого поддерева, или

• X — это вершина из правого поддерева.

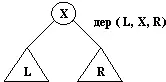
Рис. 9.5. Представление двоичных деревьев.

Эти правила непосредственно транслируются на Пролог следующим образом:

внутри( X, дер( _, X, _) ).

внутри( X, дер( L, _, _) ) :-

внутри( X, L).

внутри( X, дер( _, _, R) ) :-

внутри( X, R).

Очевидно, что цель

внутри( X, nil)

терпит неудачу при любом X.

Посмотрим, как ведет себя наша процедура. Рассмотрим рис. 9.4. Цель

внутри( X, T)

используя механизм возвратов, находит все элементы данных, содержащиеся в множестве, причем обнаруживает их в следующем порядке:

X = а; X = b; X = с; X = d

Теперь рассмотрим вопрос об эффективности. Цель

внутри( а, T)

достигается сразу же после применения первого предложения процедуры внутри. С другой стороны, цель

внутри( d, T)

будет успешно достигнута только после нескольких рекурсивных обращений. Аналогично цель

внутри( e, T)

потерпит неудачу только после того, как будет просмотрено все дерево в результате рекурсивного применения процедуры внутрико всем поддеревьям дерева T.

В этом последнем случае мы видим такую же неэффективность, как если бы мы представили множество просто списком. Положение можно улучшить, если между элементами множества существует отношение порядка. Тогда можно упорядочить данные в дереве слева направо в соответствии с этим отношением.

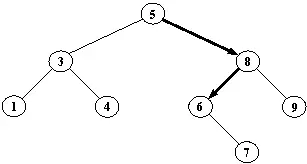
Рис. 9.6. Двоичный справочник. Элемент 6 найден после прохода по отмеченному пути 5→8→6.

Будем говорить, что непустое дерево дер( Лев, X, Прав)упорядочено слева направо, если

(1) все вершины левого поддерева Левменьше X;

(2) все вершины правого поддерева Правбольше X;

(3) оба поддерева упорядочены.

Будем называть такое двоичное дерево двоичным справочником . Пример показан на рис. 9.6.

Преимущество упорядочивания состоит в том, что для поиска некоторого объекта в двоичном справочнике всегда достаточно просмотреть не более одного поддерева. Экономия при поиске объекта X достигается за счет того, что, сравнив X с корнем, мы можем сразу же отбросить одно из поддеревьев. Например, пусть мы ищем элемент 6 в дереве, изображенной на рис. 9.6. Мы начинаем с корня 5, сравниваем 6 с 5, получаем 6 > 5. Поскольку все элементы данных в левом поддереве должны быть меньше, чем 5, единственная область, в которой еще осталась возможность найти элемент 6, — это правое поддерево. Продолжаем поиск в правом поддереве, переходя к вершине 8, и т.д.

Общий метод поиска в двоичном справочнике состоит в следующем:

Для того, чтобы найти элемент X в справочнике Д, необходимо:

• если X — это корень справочника Д, то считать, что X уже найден, иначе

• если X меньше, чем корень, то искать X в левом поддереве, иначе

• искать X в правом поддереве;

• если справочник Д пуст, то поиск терпит неудачу.

Эти правила запрограммированы в виде процедуры, показанной на рис. 9.7. Отношение больше( X, Y), означает, что X больше, чем Y. Если элементы, хранимые в дереве, — это числа, то под "больше, чем" имеется в виду просто X > Y.

Существует способ использовать процедуру внутритакже и для построения двоичного справочника. Например, справочник Д, содержащий элементы 5, 3, 8, будет построен при помощи следующей последовательности целей: