Иван Братко - Программирование на языке Пролог для искусственного интеллекта

Для работы в условиях неопределенности было придумано множество различных механизмов. Мы будем рассматривать здесь механизм, используемый в системах Prospector и AL/X для минералогической разведки и локализации неисправностей соответственно. Следует заметить, что модель, применяемая в системе Prospector, несовершенна как с теоретической, так и с практической точек зрения. Однако она использовалась на практике, она проста и может служить хорошей иллюстрацией при изложении основных принципов, а потому вполне подойдет нам, по крайней мере для первого знакомства с этой областью. С другой стороны, известно, что даже в значительно более сложных моделях не обходится без трудностей.

Достоверность событий моделируется с помощью действительных чисел, заключенных в интервале между 0 и 1. Для простоты изложения мы будем называть их "вероятностями", хотя более точный термин "субъективная уверенность". Отношения между событиями можно представить графически в форме "сети вывода". На рис. 14.14 показан пример сети вывода. События изображаются прямоугольниками, а отношения между ними — стрелками. Овалами изображены комбинации событий (И, ИЛИ, НЕ).

Мы будем считать, что отношения между событиями (стрелки) являются своего рода "мягкими импликациями". Пусть имеются два события E и H , и пусть информация о том, что имело место событие E , оказывает влияние на нашу уверенность в том, что произошло событие H . Если это влияние является "категорической импликацией", то можно просто написать

если E то H

В случае же "мягкой импликации" это отношение может быть менее определенным, так что ему можно приписать некоторую "силу", с которой оно действует:

если E то H с силой S

Та сила, с которой достоверность E влияет на уверенность в H , моделируется в системе Prospector при помощи двух параметров:

N = "коэффициент необходимости"

S = "коэффициент достаточности"

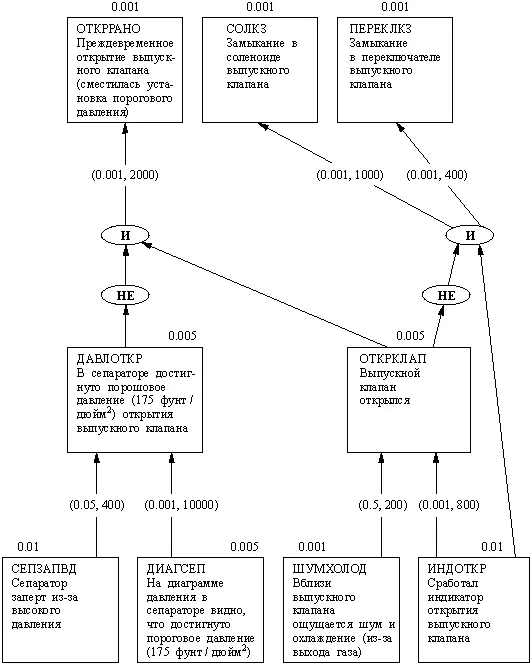
Рис. 14.14. Сеть вывода системы AL/X (заимствовано из Reiter (1980)). Числа, приписанные прямоугольникам, — априорные вероятности событий; числами на стрелках задается "сила" отношений между событиями.

В сети вывода это изображается так:

E ------------> H

(N, S)

Два события, участвующие в отношении, часто называют "фактом" и "гипотезой" соответственно. Допустим, что мы проверяем гипотезу H . Тогда мы будем искать такой факт E , который мог бы подтвердить либо опровергнуть эту гипотезу. S говорит нам, в какой степени достаточно факта E для подтверждения гипотезы H ; N — насколько необходим факт E для подтверждения гипотезы H . Если факт E имел место, то чем больше S , тем больше уверенности в H . С другой стороны, если не верно, что имел место факт E , то чем больше N , тем менее вероятно, что гипотеза H верна. В случае, когда степень достоверности E находится где-то между полной достоверностью и невозможностью, степень достоверности H определяется при помощи интерполяции между двумя крайними случаями. Крайние случаи таковы:

(1) известно, что факта E не было

(2) известно, что факт E имел место

(3) ничего не известно относительно E

Для каждого события H сети вывода существует априорная вероятность р o ( H ) (безусловная) вероятность события H в состоянии, когда неизвестно ни одного положительного или отрицательного факта. Если становится известным какой-нибудь факт E , то вероятность H меняет свое значение с р o ( H ) на p ( H|E ). Величина изменения зависит от "силы" стрелки, ведущей из E в H . Итак, мы начинаем проверку гипотез, принимая их априорные вероятности. В дальнейшем происходит накопление информации о фактах, что находит свое отражение в изменении вероятностей событий сети. Эти изменения распространяются по сети от события к событию в соответствии со связями между событиями. Например, рассмотрим рис. 14.14 и предположим, что получена информация о срабатывании индикатора открытия выпускного клапана. Эта информация повлияет на нашу уверенность в том, что выпускной клапан открылся, что, в свою очередь, повлияет на уверенность в том, что сместилась установка порогового давления.

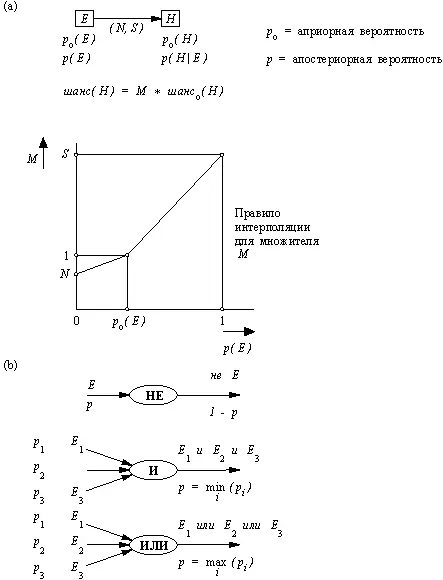
Рис. 14.15. Правила распространения вероятностей по сети, принятые в системах Prospector и AL/X: (а) "мягкая импликация" с силой ( N , S ); (b) логические комбинации отношений.

На рис. 14.15 показан один из способов реализации этого эффекта распространения информации по сети. Часть вычислений производится не над вероятностями, а над шансами . Это удобно, хотя в принципе и не обязательно. Между шансами и вероятностями имеет место простое соотношение:

шанс = вер / (1 – вер )

вер = шанс / (1 + шанс )

Пусть между E и H существует отношение "мягкой импликации", тогда, в соответствии с рис. 14.15,

шанс ( H|E ) = M * шанс ( H )

где множитель M определяется априорной и апостериорной вероятностями с учетом силы ( N, S ) связи между E и H . Предполагается, что правила Prospector'a (рис. 14.15) для вычисления вероятностей логических комбинаций событий (использующие min и max ) правильно моделируют поведение человека при оценке субъективной уверенности в таких составных событиях.

Давайте сначала расширим правила языка, с тем чтобы получить возможность работать с неопределенностью. К каждому, правилу мы можем добавить "силовой модификатор", определяемый двумя неотрицательными действительными числами S и N . Вот соответствующий формат:

Имя Правила: если

Условие

то

Заключение

с

Сила( N, S).

Примеры правил рис. 14.14 можно изобразить в этой форме так:

прав1 : если

не давлоткр и

открклап

то

открклрано

с

сила( 0.001, 2000).

прав2 : если

сепзапвд

то

давлоткр

с

сила( 0.05, 400).

Для того, чтобы произвести соответствующее расширение оболочки экспертной системы (разд. 14.5), нам понадобится внести изменения в большинство процедур. Давайте сосредоточимся только на одной из них, а именно на процедуре

рассмотреть( Цель, Трасса, Ответ)

Мы предположим, что утверждение Цельне содержит переменных (как это сделано в Prospector'e и в AL/X). Это сильно упростит дело (особенно в процедуре ответпольз). Таким образом, Цельбудет логической комбинацией элементарных утверждений. Например: