Уильям Детмер - Теория ограничений Голдратта. Системный подход к непрерывному совершенствованию
- Название:Теория ограничений Голдратта. Системный подход к непрерывному совершенствованию
- Автор:
- Жанр:
- Издательство:Array Литагент «Альпина»
- Год:2012
- Город:Москва
- ISBN:978-5-9614-1952-8, 0-87389-370-0
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Уильям Детмер - Теория ограничений Голдратта. Системный подход к непрерывному совершенствованию краткое содержание
Книга опытного консультанта Уильяма Детмера – это практическое руководство к действию, подробно описывающее процесс преобразований на любом уровне организации. С ее помощью можно определить, что нужно изменить в организации, как выявлять явные и скрытые проблемы с помощью логических деревьев и как устранять эти проблемы с помощью прорывных решений.
Книга будет интересна руководителям всех уровней, предпринимателям, а также преподавателям и студентам организационно-управленческих специальностей.
Теория ограничений Голдратта. Системный подход к непрерывному совершенствованию - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
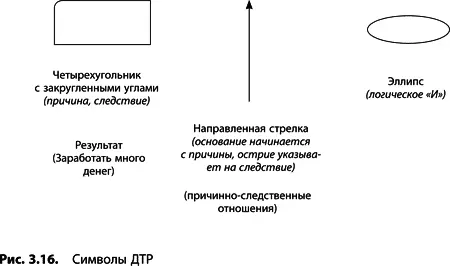
Утверждения
Во всех логических деревьях ТОС утверждения обозначаются какой-нибудь геометрической фигурой. В ДТР используются только четырехугольники с закругленными углами. В диаграмме разрешения конфликтов, дереве будущей реальности и плане преобразований применяются также и прямоугольники. В дереве перехода кроме прямоугольников вам встретятся и шестиугольники. Все эти фигуры заключают в себе утверждения, которые должны быть выражены полным предложением, содержащим законченную мысль.
Зачем нужно понятие «утверждение»?
Для чего мы пользуемся понятием «утверждение»? Если говорится, что «пропущено какое-то утверждение», значит, в логическом дереве не упомянут некий важный элемент (причина, следствие, промежуточная цель или задача и т. д.). Используя общий термин «утверждение», при анализе мы имеем возможность обозначить любой логический элемент диаграммы. Например, нежелательное явление, истинная причина, а также ключевая проблема – все эти элементы логического построения являются утверждениями в общем смысле.
Иногда в правила построения диаграммы включают фразы «соедините утверждения», «добавьте дополнительное утверждение». В этом случае речь идет именно о высказываниях, заключенных в геометрические фигуры. Но поскольку не всегда в правилах построения можно четко указать, что конкретно требуется в данной ситуации (причина, следствие и пр.), нужен какой-то обобщающий термин, каковым и является «утверждение».
Утверждения в ДТР
С деревом текущей реальности все просто: утверждения, используемые в нем, – это либо причины, либо следствия, либо и то и другое одновременно (причина одного события сама является следствием другого). Так и выстраиваются цепочки причин и следствий.
Стрелки
Стрелки используются во всех инструментах ТОС, но могут при этом обозначать совершенно различные виды связей между утверждениями. В деревьях текущей реальности, будущей реальности и плане преобразований стрелки отражают достаточность существования причины для наступления события. В диаграмме «Грозовая туча» и дереве перехода стрелки передают необходимость, но не обязательно достаточность существования первого утверждения для наступления второго (см. раздел «Необходимость и достаточность – основа построения логических деревьев» главы 2).
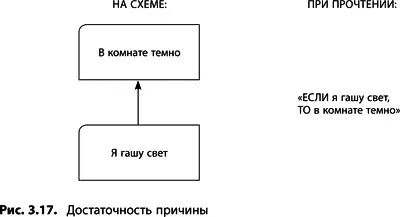
В ДТР стрелка отражает достаточность: причина, от которой начинается стрелка, является достаточной для появления результата, на который стрелка указывает. Чтобы озвучить эти отношения, нужно добавить «если» к утверждению причины и «то» к утверждению следствия:
«ЕСЛИ я выключаю свет, ТО в комнате темно».
Однако нужно быть осторожным с использованием и чтением стрелок в ДТР. В приведенном примере скрывается ловушка (рис. 3.17): подразумевается, что, во-первых, за пределами комнаты темно (сейчас ночь) и, во-вторых, в комнате нет окон или других отверстий, пропускающих свет. Эти предположения не включены в логическое построение, но они присутствуют и непосредственно влияют на правильность установленных связей.
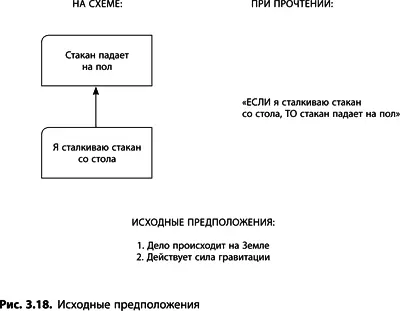
Исходные предположения
За каждой стрелкой в ДТР лежат некие не озвученные, но обязательно существующие предположения, касающиеся рассматриваемой ситуации в целом, граничных условий или физики явлений. Рассмотрим пример из двух утверждений, связанных стрелкой (рис. 3.18):
«ЕСЛИ я столкну стакан со стола, ТО он упадет на пол».
При этом подразумевается, но не говорится о том, что на объекты действует сила притяжения Земли. Вы, наверное, подумаете: «Ну, конечно, это само собой разумеется, она действует всегда». Но сила притяжения важна не всегда. Космонавтам на орбите не приходится волноваться о том, что стакан упадет на пол; скорее им нужно беспокоиться, что он куда-нибудь улетит, ведь в этом случае исходная предпосылка (наличие гравитации) не работает. В результате при смене исходных условий мы можем получить разные результаты. Когда строите или анализируете логические деревья, не забывайте проверять, какие предположения важны для корректности каждой прорисованной связи и имеют ли смысл указанные причинно-следственные отношения в данных условиях. Более подробно об анализе причинно-следственных связей говорится в главе 2 «Критерии проверки логических построений».
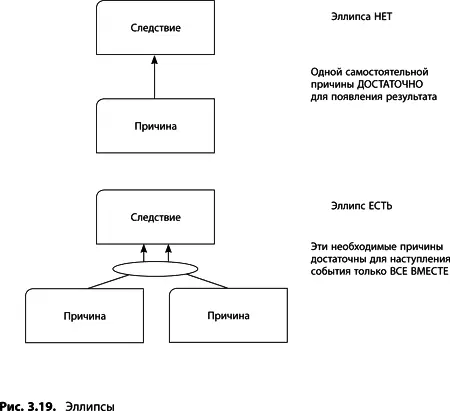
Эллипсы
Эллипс применяют в диаграммах, использующих логическое «И» (дерево текущей реальности, будущей реальности, перехода). Его задача – объединить несколько необходимых причин, которые в совокупности достаточны для возникновения некоторого результата (рис. 3.19). Если отсутствует любая из причин, объединенных эллипсом, то не будет иметь место и следствие этих причин, т. е. причинно-следственная связь нарушается. На практике разработчики пропускают сам эллипс, т. е. упускается существенное условие наступления некоторого события.
Вспомним недавний пример: «ЕСЛИ я выключаю свет, ТО в комнате темно». Вероятно, чтобы в комнате стало темно, недостаточно просто выключить свет (рис. 3.20). Можно добавить еще причину «ЕСЛИ в комнате нет окон», но и этого недостаточно, поэтому прибавляем «ЕСЛИ единственная в комнате дверь закрыта». Вот теперь это «строгое» построение.
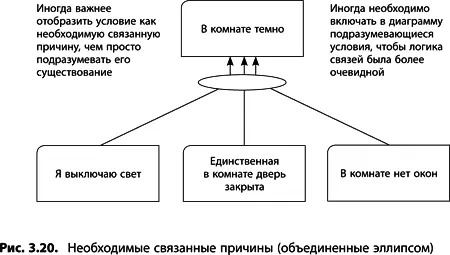
Помните, мир многогранен. У большинства явлений несколько причин, самостоятельных или взаимозависимых. Самостоятельной считается причина, которой самой по себе достаточно для наступления события. Если у одного явления имеется несколько самостоятельных причин, их обычно называют альтернативными (см. раздел «Альтернативная причина» в главе 2). Необходимая, но не достаточная причина может привести к появлению следствия только в совокупности с другими факторами, объединенными на рисунке эллипсом. Необходимо тщательно проверять существование связей и зависимостей между уже выстроенными утверждениями.
Примечание:нет необходимости включать в ДТР все до последней предпосылки или условия наступления события, иначе процесс построения сильно затянется и результат получится плохо читаемым. Всегда нужно ориентироваться на аудиторию, для которой вы создаете диаграмму. Если только для себя и в сфере, в которой вы хорошо ориентируетесь, можно многое помнить, не указывая на рисунке. Если же вам предстоит демонстрировать логическое дерево перед широкой аудиторией, подумайте, что именно вашим слушателям известно об изучаемом вопросе. Обычно представляемые публике диаграммы должны быть более подробными (меньше скрытых предположений; больше логических условий, объединенных эллипсом) – это поможет избежать недопонимания и путаницы.
Читать дальшеИнтервал:
Закладка:









