Дэвид Дойч - Начало бесконечности. Объяснения, которые меняют мир

Подобно тому, как добавлением пиктограмм можно было расширять словарь древней системы письма, добавлением символов можно было расширить диапазон системы записи чисел, что и делалось. Но в получающейся системе всегда был символ с самым большим значением, а значит, она не была универсальной в плане совершения арифметических операций без поштучного пересчета.

Единственный способ освободить арифметику от «палочек» – использовать правила с универсальной сферой применимости. Как и с алфавитами, достаточно будет небольшого набора базовых правил и символов. В универсальной системе, которой все пользуются сегодня, десять символов, это цифры от 0 до 9, а своей универсальностью она обязана правилу, в соответствии с которым значение цифры зависит от ее положения в числе. Например, цифра 2 означает два, если она сама по себе, но двести, если она присутствует в числе 204. В таких «позиционных» системах нужны «заполнители» разрядов, как, например, цифра 0 в числе 204, единственная функция которой – сдвинуть двойку в позицию, означающую «двести».

Эта система зародилась в Индии, но когда именно, неизвестно. Возможно, это случилось лишь в девятом веке, поскольку до этого она вроде как встречается только в нескольких неоднозначных документах. Так или иначе, ее огромный потенциал для науки, математики, техники и торговли широко не осознавался. Примерно в то же время ее взяли на вооружение арабские ученые, но в обиход в арабском мире она вошла только через тысячу лет. Любопытное отсутствие стремления к универсальности повторилось и в средневековой Европе: индийские цифры были переняты у арабов лишь несколькими учеными в десятом веке (и в результате были ошибочно названы «арабскими цифрами»), но в повседневное использование они вошли только столетия спустя.

Уже к 1900 году до нашей эры древние вавилоняне изобрели в сущности универсальную систему счисления, но и они вполне могли не задумываться об универсальности и даже вовсе о ней не знать. Это была позиционная система, но очень громоздкая по сравнению с индийской. В ней было 59 «цифр», каждая из которых записывалась как число в системе типа римской. Пользоваться ею для совершения арифметических операций с числами в повседневной жизни было еще сложнее, чем римскими цифрами [30]. В этой системе также не было символа для нуля, а вместо заполнителей использовались пробелы. Изобразить ноль в конце строки было никак нельзя, эквивалента десятичной запятой тоже не было (это все равно что в нашей системе числа 200, 20, 2, 0,2 и так далее все записывались бы как 2, и различить их можно было бы только по контексту). Все это наводит на мысль, что при разработке системы задача добиться универсальности не была основной, и когда она была достигнута, ее особо не оценили.

Возможно, понять эту странную закономерность позволит примечательный случай, произошедший в третьем веке до нашей эры с древнегреческим ученым и математиком Архимедом. В ходе своих исследований в области астрономии и чистой математики он столкнулся с необходимостью производить арифметические операции с достаточно большими числами, и ему пришлось изобрести свою собственную систему записи. Он отталкивался от греческой, с которой был знаком и которая была похожа на римскую [31], только в ней символ с наибольшим значением обозначался через M – 10 000 (один мириад). Диапазон системы уже был расширен правилом, предписывающим умножать на десять тысяч число, написанное над M. Например, двадцать обозначалось символом κ, а четыре – δ, и двадцать четыре мириада (240 000) можно было записать как .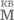

Если бы только по этому правилу можно было создавать многоуровневые числа, чтобы 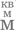означало бы 24 мириада мириадов, система стала бы универсальной. Но, очевидно, греки до этого так и не дошли [32]. И, что более удивительно, не дошел и Архимед. Его система строилась на другой идее, напоминающей современное «экспоненциальное представление» (когда, скажем, два миллиона записываются как 2×106), только в степень возводилось не десять, а мириад мириадов (100 000 000). Но в этом случае требовалось, чтобы число, являвшееся показателем степени (в которую возводились сто миллионов), существовало в греческой системе. Другим словами, показатель степени не мог превышать сто миллионов или около того. Значит, эта конструкция иссякала после числа, которое мы бы записали как 10800 000 000. Если бы не это дополнительное правило, у Архимеда получилась бы универсальная система, хотя и неоправданно неуклюжая.

Даже сегодня числа, больше 10800 000 000, могут пригодиться разве что математикам, и то очень редко. Но вряд ли Архимед наложил свое ограничение из-за этого, потому что на этом он не остановился. Продолжив исследовать понятие чисел, он добавил еще одно расширение, на этот раз получилась еще более странная система с основанием 10800 000 000. Но снова он разрешил возводить это число только в степени, не превышающие 800 000 000, устанавливая таким образом произвольный предел где-то после 106,4×1017.

Зачем? Сегодня кажется, что, накладывая ограничение на то, какие символы можно использовать в его числовой записи и в каких позициях, Архимед просто упрямствовал в своих заблуждениях. Для этого нет никакого математического оправдания! Но если бы Архимед захотел позволить применять свои правила без произвольных ограничений, он мог бы изобрести гораздо более удачную универсальную систему, просто убрав произвольные ограничения из существовавшей тогда греческой системы. (Несколькими годами позже математик Аполлоний придумал еще одну систему записи чисел, которой точно так же не хватало универсальности. Такое впечатление, что в античном мире все намеренно ее избегали!)

Вот что писал об индийской системе математик Пьер-Симон Лаплас (1749–1827): «Мы должны оценить грандиозность этого достижения, вспомнив, что до него не додумались Архимед и Аполлоний, два величайших ума античного мира». Но верно ли, что они не додумались до этого понятия? Может, они просто предпочли держаться от него подальше? Архимед должен был понимать, что метод расширения системы записи чисел, которым он воспользовался два раза подряд, можно продолжать до бесконечности. Но, возможно, он сомневался, что получившиеся в результате записи обозначали что-либо пригодное для разумного обсуждения. Действительно, одним из мотивов для всего этого начинания было желание опровергнуть идею, трюизм того времени, что песчинки на пляже сосчитать невозможно. И Архимед воспользовался своей системой, чтобы подсчитать, сколько песчинок понадобилось бы, чтобы заполнить всю небесную сферу. Это наводит на мысль, что ни у него, ни в древнегреческой культуре в целом, могло не быть в принципе понятия абстрактного числа, и для них такие записи могли относиться только к объектам, хотя бы и воображаемым. В этом случае универсальность была бы сложным для постижения свойством, что уж говорить о том, чтобы к ней стремиться. А может Архимед просто почувствовал, что если он хочет получить убедительный результат, то ему лучше не стремиться к бесконечной сфере охвата. Так или иначе, хотя с нашей точки зрения в системе Архимеда несколько раз «намечался» скачок к универсальности, он, очевидно, к этому не стремился.