Дэвид Дойч - Начало бесконечности. Объяснения, которые меняют мир

Другими словами, финитизм, как и инструментализм, – это не что иное, как план, цель которого помешать достижению прогресса в понимании сущностей, выходящих за рамки непосредственного опыта. А значит, и достижению прогресса вообще, ведь, как я объяснил, в рамках нашего «непосредственного опыта» сущностей нет.

Все вышеприведенное обсуждение предполагает универсальность разума . Сфера досягаемости науки имеет неотъемлемые ограничения; это относится и к математике, и к любому направлению философии. Но если вы считаете, что существуют границы той области, в которой разум есть должный судья идей, значит, вы верите в иррациональное или в сверхъестественное. Аналогично если вы отрицаете бесконечное, то вы застряли в конечном, а конечно парохиально. Здесь нельзя остановиться посередине. Самое разумное объяснение чего бы то ни было в конечном счете включает в себя универсальность, а значит, и бесконечность. Сферу объяснимого нельзя взять и ограничить в приказном порядке.

Одним из проявлений этого в математике стал принцип, впервые явно сформулированный в девятнадцатом веке математиком Георгом Кантором, согласно которому абстрактные сущности можно определить любым желаемым способом через другие сущности при условии, что определения однозначны и непротиворечивы. Кантор заложил основы современного математического исследования бесконечности. В двадцатом веке его принцип отстаивал и обобщал математик Джон Конуэй, который дал ему эксцентричное, но вполне подходящее название – движение за освобождение математиков . Согласно Конуэю, открытия Кантора встретили резкое неприятие со стороны современников, включая большинство математиков того времени и также многих ученых, философов – и богословов. Как это ни парадоксально, религиозные возражения по сути строились на принципе заурядности. Попытки понять бесконечность и работать с ней в них характеризовались как посягательство на прерогативу Бога. В середине двадцатого века, через много лет после того, как исследования в области бесконечности стали обычным для математики делом и нашли в ней бесчисленное множество приложений, философ Людвиг Виттгенштейн все еще презрительно осуждал их за «бессмысленность». (Правда, в конечном итоге он предъявил это обвинение и философии в целом, включая свою собственную работу, см. главу 12.)

Я уже упоминал другие примеры принципиального неприятия бесконечности. Необъяснимую антипатию к универсальным системам записи чисел выражали Архимед, Аполлоний и другие. Существуют такие учения, как инструментализм и финитизм. Принцип заурядности начинает с того, чтобы уйти от ограниченности взглядов и добраться до бесконечности, но в итоге загоняет науку в бесконечно малый, непредставительный пузырь постижимости. Есть еще пессимизм, который (как будет показано в следующей главе) стремится объяснить неудачи существованием конечной границы совершенствования. Один из примеров пессимизма – парадоксальная парохиальность сравнения Земли со звездолетом – транспортным средством, которое гораздо лучше подошло бы в качестве метафоры бесконечности.

Всякий раз обращаясь к бесконечности, мы опираемся на бесконечную сферу применимости какой-либо идеи. Всегда, когда идея бесконечности имеет смысл, это связано с тем, что существует объяснение, каким образом некий конечный набор правил для манипулирования конечными символами ссылается на нечто бесконечное. (Повторю, что это также лежит в основе всех остальных наших знаний.)

В математике бесконечность изучается посредством бесконечных множеств (то есть множеств с бесконечным числом элементов). Определяющее свойство бесконечного множества заключается в том, что некоторая его часть содержит столько же элементов, сколько все оно целом. Возьмем, например, натуральные числа:

В верхней строке на рисунке каждое натуральное число встречается ровно один раз. В нижней строке содержится только часть этого множества: натуральные числа, начиная с 2. Чтобы показать, что в этих двух множествах одинаковое число элементов, на рисунке между ними установлено соответствие, которое математики называют «взаимно однозначным».

Чтобы проиллюстрировать некоторые интуитивные вещи, от которых приходится отказаться, рассуждая о бесконечности, математик Давид Гильберт придумал мысленный эксперимент. Он представил себе гостиницу с бесконечным числом номеров: отель «Бесконечность» . Номера пронумерованы с помощью натуральных чисел, начиная с 1 и заканчивая… Чем же?

Число на двери последнего номера отеля – не бесконечность. Во-первых, последнего номера вообще нет. Мысль о том, что в любом пронумерованном множестве гостиничных номеров есть элемент с наибольшим числом на двери, – это первое интуитивное представление из повседневной жизни, которое придется отбросить. Во-вторых, в любой конечной гостинице, в которой номера пронумерованы от 1, будет один под номером, равным общему их числу, а также другие с близкими номерами: если бы номеров было десять, на двери одного из них стояло бы десять, а среди остальных был бы номер девять. Но в отеле «Бесконечность», в котором число номеров бесконечно, порядковые номера их всех бесконечно далеки от бесконечности.

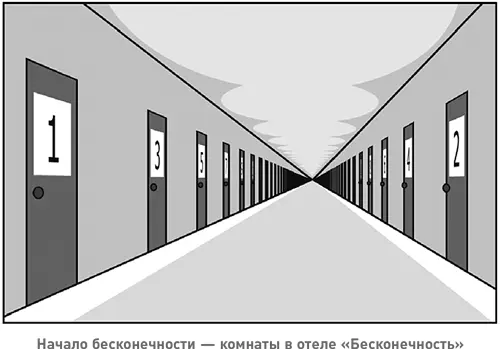
Теперь представьте, что отель заполнен. В каждом номере может жить один и только один человек. Когда «заполнена» конечная гостиница, это все равно что «свободных мест нет». Но в отеле «Бесконечность» место найдется всегда. Одно из условий пребывания в нем – постояльцам придется сменить номер, когда администратор их об этом попросит. По прибытии нового гостя по системе оповещения проходит сообщение: «Просим всех постояльцев немедленно переехать в номер, на двери которого число на единицу больше, чем на двери занимаемого вами сейчас номера». Таким образом, по схеме, представленной на первом в этой главе рисунке, тот, кто жил в номере 1, переезжает в номер 2, а тот, кто жил в номере 2, – в номер 3 и так далее. Что же происходит в последнем номере? Но ведь последнего нет, и такого вопроса просто не возникает. Вновь прибывший заселяется в номер 1. Бронировать место в отеле «Бесконечность» не нужно.

Очевидно, в нашей Вселенной не может быть такого места, как отель «Бесконечность», поскольку в нем нарушается несколько законов физики. Однако это математический мысленный эксперимент, поэтому единственное ограничение на воображаемые законы физики – их непротиворечивость. И из-за этого требования непротиворечивости они контринтуитивны: в интуитивных вещах, касающихся бесконечности, часто отсутствует логика.