Ричард Докинз - Рассказ предка. Паломничество к истокам жизни

Если отступить от времени Homo ergaster еще на 1 млн лет в прошлое, у нас не останется сомнений в том, на каком континенте следует искать свои корни. Ученые (включая сторонников “мультирегионального” происхождения человека) согласны в том, что это – Африка. Самые убедительные находки костей указанного возраста обычно относят к H. habilis. Некоторые авторитетные ученые выделяют еще один современный ему вид – H. rudolfensis. Другие отождествляют его с кениапитеком, описанным Лики и его коллегами в 2001 году. Есть специалисты, которые вообще предпочитают не давать этим окаменелостям видовые названия, а просто относят их всех к “раннему Homo”. У меня нет по этому вопросу четкой позиции. Мне важнее люди из плоти и крови, и я буду называть их “умелыми”. Ископаемые остатки людей умелых старше, чем остатки людей работающих, и их сохранилось меньше. Череп самой хорошей сохранности имеет номер KNM-ER 1470. Его хозяин жил около 1,9 млн лет назад.

H. habilis столь же сильно отличался от человека работающего, как человек работающий – от нас самих. Существуют также промежуточные формы, которые довольно трудно классифицировать. Череп H. habilis был не таким прочным, как у человека работающего, а надбровные дуги не были так сильно выражены. В этом отношении H. habilis были похожи на нас, и это не удивительно. Прочность черепа и надбровные дуги, судя по всему, относятся к признакам, которые (например, волосы) гоминиды могут терять или приобретать по малейшему эволюционному поводу. Начиная с H. habilis , наш мозг увеличивался. Точнее, его размеры начали превышать средние размеры мозга других человекообразных обезьян – хотя и у них мозг уже был довольно крупным. Именно поэтому человека умелого относят к роду Homo. Для многих палеонтологов крупный мозг – отличительный признак нашего рода. H. habilis, объем мозга которого превысил 750 см 3, перешел Рубикон и стал человеком.

Я не люблю “рубиконы”, “рубежи” и “промежутки”. В частности, нет оснований полагать, что ранний H. habilis отличался от предшественника сильнее, чем от преемника. Эта мысль может показаться здравой, потому что предшественник носит другое родовое название (австралопитек), а преемник (H. ergaster) – просто “другой Homo”. Конечно, если мы рассматриваем современные виды, мы ждем, что представители разных родов будут меньше похожи, чем представители разных видов в пределах одного рода. Однако в случае окаменелостей это не работает, потому что там имеется непрерывный ряд поколений. На границе между любым ископаемым видом и его непосредственным предшественником всегда найдутся особи, о которых можно спорить бесконечно. Потому что, если воспользоваться методом доведения до абсурда, окажется, что родители, принадлежащие к одному виду, породили потомство, принадлежащее уже к другому виду. Еще более нелепо предположение о том, что ребенок рода Homo появился у родителей совершенно другого рода – австралопитеков. Таким образом, в этой области науки об эволюции правила таксономии не работают.

Отказ от названий позволяет рассуждать о том, почему мозг внезапно начал расти. Как оценить увеличение мозга гоминид и построить график зависимости среднего размера мозга от геологического времени? С единицами времени проблем не возникает: это должны быть миллионы лет. С размером мозга сложнее. Ископаемые черепа и слепки позволяют оценивать размер мозга в кубических сантиметрах, которые потом довольно легко перевести в граммы. Однако нам не обязательно нужен абсолютный размер мозга. У слона мозг крупнее нашего, и тем не менее мы с полным правом считаем себя умнее. Мозг тираннозавра был ненамного меньше нашего, однако это не мешает считать динозавров глупыми: относительный размер нашего мозга больше.

Можно вносить поправку на абсолютный размер и выражать размер мозга как функцию от размера, который “должен” иметь мозг при данном размере тела. Эта тема достойна отдельного рассказа.

Итак, мы хотим оценить размер мозга животного – например Homo habilis: больше он или меньше, чем “должен быть” при данном размере тела? Мы допускаем (я – не очень охотно, но так и быть), что у крупных животных мозг должен быть крупным, а у малых – маленьким. Мы, тем не менее, желаем знать, бывают ли одни виды “мозговитее” других. Как рассчитать поправку на размер тела? Нам нужно сформулировать разумный принцип, согласно которому мы сможем вычислить прогнозируемый размер мозга животного на основе размера его тела. И тогда мы сможем сопоставить реальный размер мозга с прогнозируемым.

Эти вопросы могут относиться к любой другой части тела. Бывает ли так, что сердца, почки или лопатки у некоторых животных крупнее (или мельче), чем должны быть? Если да, то можно предположить, что их образ жизни требует специального размера сердца (почки, лопатки и так далее). Нам известен общий размер его тела. При этом не забывайте, что “должен быть” в данном случае не означает “необходим по функциональным причинам”. Это означает “прогнозируемый размер, полученный на основе сравнения с похожими животными”. Поскольку это “Рассказ Человека умелого”, а самая замечательная черта H. habilis – его мозг, то обсуждать этот вопрос мы будем на примере мозга. Но это не помешает нам получить более общие выводы.

Начнем с диаграммы рассеяния массы мозга относительно массы тела для большого количества видов. Каждый символ на графике (его построил мой коллега, выдающийся антрополог Роберт Мартин) обозначает один современный вид млекопитающих – всего их на графике 309, и расположены они от меньшего к большему. (H. sapiens – значок со стрелкой, а значок рядом – это дельфин.) Жирная линия, соединяющая точки, представляет собой прямую, которая, согласно статистическим расчетам, максимально приближена ко всем точкам.

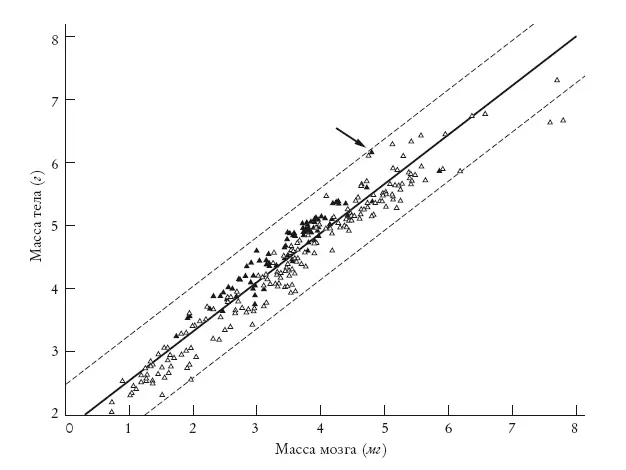
Логарифмическое соотношение массы головного мозга и тела у различных видов плацентарных млекопитающих. Закрашенные треугольники обозначают приматов. Стрелкой обозначен человек. Martin [185].

Небольшое затруднение, смысл которого сейчас станет понятен, заключается в том, что обе шкалы графика лучше делать логарифмическими. Именно так построен этот график. Здесь видна зависимость логарифма массы мозга животного от логарифма массы его тела. Логарифмическия шкала означает, что шаги, отложенные по горизонтальной (или вертикальной) оси, представляют собой значения, умноженные на некоторое число, например на десять, а не просто последовательный ряд значений. Логарифм с основанием десять удобен тем, что мы можем рассматривать его как количество нулей в числе. Если для того, чтобы получить массу слона, нужно умножить массу мыши на миллион, то это значит, что нужно прибавить к массе мыши шесть нулей, то есть нужно добавить шесть к логарифму первого, чтобы получить логарифм второго. На полпути между ними на логарифмической шкале – в трех нулях – находится животное, которое весит в тысячу раз больше мыши и в тысячу раз меньше слона: например человек. Круглые числа, например тысяча и миллион, легче для понимания. “Три с половиной нуля” лежат где-то между тысячей и десятью тысячами. Заметьте, что “на полпути” по отношению к нулям – это не то же самое, что “на полпути между” по отношению к граммам. В нашем случае это делается автоматически благодаря подсчету логарифмов чисел. Логарифмические величины применяют для интерпретаций простых арифметических величин.