Ричард Суинберн - Существование Бога

Всё это проясняется основной теоремой теории подтверждения – теоремой Байеса 11, которая выглядит следующим образом

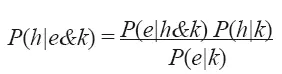
Эта теорема напрямую следует из аксиом, на которых построена математическая теория вероятности, поскольку их истинность покоится на независимых основаниях 12. Но обращаясь к этой теореме в дальнейшем, я буду апеллировать главным образом не к этим основаниям, а больше к тем, которые были изложены в этой главе (хотя конкретный способ, с помощью которого Р ( h|e&k ) повышается при P ( h|k ) и Р ( e|h&k ), но понижается при P ( e|k ), не зависит от чего-либо, о чем я говорил до сих пор, но должен зависеть от самого объекта).

P ( h|k ), предварительная вероятность, которой обладает h , в нормальном случае зависит, как мы уже поняли, как от внутренней простоты h (и ее ограниченного диапазона), так и от того, насколько хорошо h согласуется с нашим общим фоновым знанием о мире, которое содержится в k . Однако, как мы увидели в 1 главе, любое распределение данных между е и k будет совершенно произвольным.

Обычно удобнее всего рассматривать самую последнюю наблюдаемую часть данных е и остальное к, но иногда удобно допустить, что е – это все наблюдаемые данные, а к – просто «тавтологические данные». В последнем случае предварительная вероятность P(h|k) – это то, что я буду называть «внутренней (intrinsic) вероятностью» гипотезы Zz, она будет зависеть главным образом от простоты h (а также в меньшей степени – от узости диапазона). Но если к содержит логически вероятные данные об устройстве мира, то P(h\k) будет зависеть также от того, насколько хорошо h согласуется с этими данными. В том случае, если к – это просто «тавтологическая данность», Р(е\к) будет тем, что я назову в дальнейшем «внутренней вероятностью» е.

Я сказал о том, что теорема Байеса истинна, но мне следует пояснить, что я подразумеваю, говоря это. Я имею в виду, что в той мере, в которой различные е, h и к могут быть выражены численно, будет справедливо устанавливать численные отношения между ними. А в той мере, в которой они не могут быть точно выражены численно, мое заявление о том, что теорема Байеса истинна, будет просто заявлением, что все утверждения сравнительной вероятности, которые следуют из этой теоремы, истинны. Под утверждениями сравнительной вероятности я подразумеваю утверждения о том, что одна вероятность больше, такая же или меньше другой вероятности (иногда такие утверждения – это всё, что мы можем более или менее оправданно сказать о некоторых вероятностях: см. с. 42–43). Так, из теоремы Байеса следует, что если даны две гипотезы h 1и h 2, при которых Р ( e|h 1 &k ) = Р ( e|h 2 &k ), то Р ( e|h 1 &k ) > Р ( e|h 2 &k ), если и только если P ( h 1 |k ) > P ( h 2 |k ). Иными словами, если обе гипотезы h x и h 2 полагают равную вероятность того, что мы обнаружим некую данность е, при заданном фоновом знании к, тогда одна из них, h 1, будет более вероятна, чем другая, по всей совокупности данных е и к, если и только если h 1 была более вероятна, чем h 2 только с учетом фоновых данных. Выразим это более формально: если h 1 и h 2 обладают равной предсказательной силой, h 1 будет обладать большей апостериорной вероятностью (то есть вероятностью по всей совокупности данных е и к), чем h 2, если и только если: она повышает предварительную вероятность. Так, например, если нам даны две научные теории, с равным успехом предсказывающие некоторые наблюдаемые данные, то одна из них будет более вероятна, чем другая, если и только если она была более вероятной еще до того, как наблюдения были произведены. Или, опять же, из теоремы Байеса следует, что если P ( h 1 |k ) = P ( h 2 |k ), то Р ( h 1 |e&k ) > Р ( h 2 |e&k ), если и только если Р ( e|h 1 &k ) > Р ( e|h 2 &k ). Это означает, что если две гипотезы равновероятны до того, как получены некоторые данные е, одна из них будет более вероятна, чем другая, по всей совокупности данных, если и только если согласно этой гипотезе то, что е будет обнаружено, будет более вероятно, чем согласно другой гипотезе (в крайнем случае, h 1может влечь за собой е – оно может быть дедуктивным следствием h 1, а h 2может влечь за собой ¬ e , то есть то, что е не произойдет).

Рассмотрим еще один пример, чуть отличный от приведенных выше и иллюстрирующий действие теоремы Байеса. Пусть h – это гипотеза о том, что Джонс ограбил Барклайс Банк, е – это данные о том, что он находился около банка в момент совершения преступления, а k – это фоновое знание о том, что Джонс уже однажды ограбил другой банк (Ллойдс Банк). Тогда Р ( h|e&k ) будет определяться объяснительной силой h , отношением Р ( e|h&k ) к P ( e|k ), и предварительной вероятностью h , то есть P ( h|k ). Р ( h|e&k ) – это вероятность пропозиции е при данных h и k . В данном случае она равна 1, поскольку, если Джонс ограбил этот банк, он должен был находиться в это время рядом с местом преступления. P ( e|k ) – это вероятность того, что он будет находиться в это время рядом с местом преступления, с учетом того, что он уже ограбил Ллойдс Банк. Она будет выше, чем P(h\k), то есть вероятность того, что Джонс ограбил Барклайс Банк, при условии, что он уже ограбил Ллойдс Банк, поскольку он мог находиться там по совершенно невинному поводу. Следовательно, вероятность того, что он ограбил Барклайс Банк – это предварительная вероятность того, что он это совершил, возрастающая в той мере, в которой гипотеза о том, что он это совершил, делает е более вероятным, чем если бы он его не ограбил.

На этом этапе будет полезно, прежде чем продолжить рассмотрение главного аргумента, сделать еще одно важное замечание относительно утверждения, которое иллюстрирует теорема Байеса. Иногда считается, что мы соглашаемся с той или иной гипотезой только в том случае, если у нас есть возможность ее проверить, может ли она предсказывать определенные события, после чего мы смотрим, произойдут эти события или нет. И только если они произошли, мы соглашаемся принять эту гипотезу. Однако мне кажется, что, хотя мы часто проверяем гипотезы таким образом, нам не следует устанавливать их вероятность на основе очевидности и потому принимать их. Теорема Байеса, конечно же, не подразумевает утверждение (понятое в указанном выше буквальном смысле), что гипотезы должны успешно предсказывать в том случае, когда их вероятность устанавливается на основе очевидности. Согласно этой теореме, совершенно неважно, наблюдается ли е до или после того, как была сформулирована h. Имеют значение только отношения вероятности, существующие между е и h . И, разумеется, теорема верна в этом отношении. То, что я называю Р ( e|h&k ) «предсказательной силой», которой обладает h, не подразумевает, что е было обнаружено лишь для того, чтобы постулировать h, предсказавшую его.